Wielomiany

1.Definicja wilomianu - Wilomian jest to funkcja w postaci:

W(x)=a_nxⁿ+a_n-1x^n-1+...+a₂x²+a₁x¹+a₀x⁰

a_kx^k - wyraz stopnia k; a_k - współczynnik wyrazu stopnia k; a₀x⁰ = a₀ - wyraz wolny; n- stopień W(x)
W(x) = 6x⁵ - 2x⁴ + 3x² - x + 7 gdzie: -2x⁴ - wyraz 4 - stopnia; 3 - współczynnik przy x²; 7 - wyraz wolny
W(x) = 6x⁵ - 2x⁴ + 0x³ + 3x² - x + 7 wielomian uzupełniony do pełnego; 5 - stopień wielomianu

2. Równania wielomianowe
Równanie wielomianowe otrzymujemy przyrównując wielomiany do zera.
W(x) = 2x³ - 3x² + 3x - 2 = 0

3. System twierdzeń o miejscach zerowych:
I Twierdzenie o ilości pierwiastków (rozwiązań) równania wielomianowego.
n - parzyste ;W(x) stopnia parzystego może mieć od 0 do n pierwiastków
n - nieparzyste; W(x) stopnia nieparzystego może mieć od 1 do n pierwiastków

II Twierdzenie o rozkładzie wielomianu na czynniki.
Każdy wielomian można rozłożyć na funkcje liniowe i kwadratowe.
W(x) da się rozłożyć na czynniki stopnia pierwszego i drugiego.
Nie znaleziono ogólnej metody na dokonywanie powyższego rozkładu.

4. Metody rozkładania wielomianu na czyniki.
a) Gdy a₀ = 0 to wyłanczamy x przed nawias: 2x³ - 4x² - x = 0   →  x(2x² - 4x - 1) = 0 ⇔  x = 0 ∨ 2x² - 4x - 1 = 0
b) Gdy współczynniki są odpowiednio dobrane, rozkładamy przez podwójne wyłączanie przed nawias.
x³ + 3x² - 4x - 12 = 0
x²(x+3) - 4(x+3) = 0
(x+3)(x² - 4 x) = 0  ⇔x + 3 = 0 ∨ x² - 4x=0
c) Rozkład poprzez dziedzlenie. Umożliwia to następujący system twierdzeń.

III Twierdzenie o pierwiastkach całkowitych wielomianu.
Jeżeli wielomian ma pierwiastek całkowity to musi on dzielić wyraz wolny.
x³ - 9x² + 15x - 7 = 0 jeżeli x₀ ∈ C ⇒ x₀ | 7 czyli x₀∈{±1,±7}
Spr. W(1) = 1 - 9 + 15 - 7 = 16 - 16 = 0

IV Twierdzenie o pierwiastkach wymiernych

x₀ ∈ W ⇒ x₀ = n/m ∧ n | a₀ ∧ m | a_n
2x³ - 5x² - 4x + 3 = 0
x₀ ∈ W => x₀ = n/m ∧ n | 3 ∧ m | 2 => x₀ ∈ {±&u1-2;;±1&u1-2;}

V Twierdzenie o podziale wielomianów - Tw.Bezou
W(x₀) = 0 ⇔ (x-x₀) | W(x)
x₀ jest pierwiastkiem wielomianu ⇔ gdy wielomian jest podzielny przez (x-x₀)
W(x) = 2x³ - 5x -4x + 3; x₀ ∈ { ±1;±3}-III Tw.
W(3) = 2*27 - 5*9 - 12 + 3 = 54 - 45 -12 + 3 = 57 - 57 = 0
dzielnik W(x) to (x-3), po przeprowadzeniu dzielenia wynik jest równy 2x² + x - 1
W(x) = (x - 3)*(2x² + x -1) = 0 ⇔ (x-3) = 0 ∨ (2x²+ x - 1) = 0

5.NIerówności wielomianowe

a) Aby rozwiązać nierówność W(x)≥  0 rozwiązujemy najpierw równanie:
W(x) = 0

b) Rozkładamy zatem wielomiany na czynniki liniowe i kwadratowe W(x) = W¹ * W²...
Znajdujemy wszystkie miejsca zerowe, zwracając uwagę na krotność pierwiastków.
W(x) = (x-2)(x-2)(x² + 5) x₀=2 pierwiastek dwukrotny

c) szkicujemy wykres wielomianu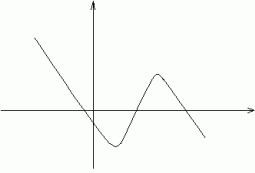

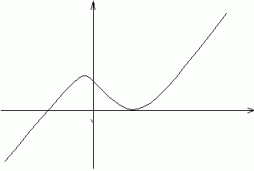
Jest to wykres typu "fala" zależy od stopnia wielomianu.
Przy szkicowaniu bierzemy pod uwagę znak przy najwyższej potędze "x", wykres szkicujemy od prawej strony.
W miejscach zerowych o nieparzystej krotność wielomian zmienia znak!
Niech W(x) = (x-1)(x-2)(x-2)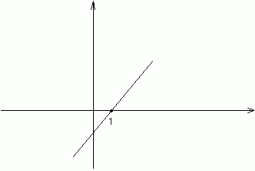

(zmienia znak i przecina oś)
natomiast w miejscu zerowym o parzystej krotności wielomian nie zmienia znaku.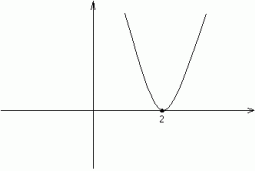

(nie zmienia znaku, dotyka osi - odbija się od osi)

d) zaznaczamy znaki na wykresie.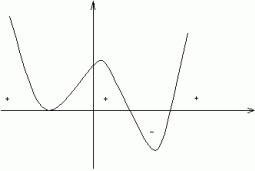

- znaki robimy między wykresem a osią X.
- odczytujemy potrzebne przedziały w których wielomian przybiera odpowiedajace nierówności wartości.