Funkcja homograficzna
Funkcja homograficzna jest funkcją wymierną, mającą postać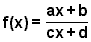
Liczby a, b, c i d są ustalone, przy czym liczba c<>0. Dlaczego liczba c musi być różna od zera - ponieważ jak by była równa zeru to mianownik byłby liczbą stałą i dany iloraz byłby tylko funkcją liniową. Jest jeszcze jedna własność, którą muszą spełniać te liczby, a mianowicie tzw. wyznacznik D=a*d-b*c<>0. Chodzi o to, aby licznik i mianownik nie miały w sobie takiej samej funkcji liniowej, co po skróceniu dałoby funkcję stałą. Dziedziną funkcji homograficznej jest zbiór wszystkich miczb rzeczywistych oprócz liczby będącej miejscem zerowym mianownika (DÎR\{-d/c}). Natomiast przeciwdziedziną jest zbiór DÎR\{a/c}. Miejscem zerowym tej funkcji jest x0=-b/a. Jeżeli liczba b jest równa zeru, to funkcja nie ma miejsca zerowego. Wykresem funkcji homograficznej jest hiperbola.
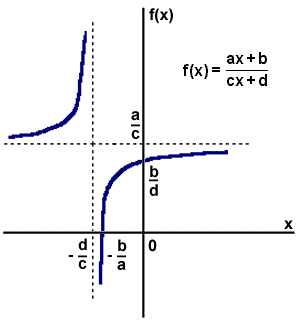
Hiperbola ma dwie asymptoty (poziomą i pionową). Asymptota pozioma jest funkcją stałą wyrażoną wzorem f(x)=a/c, natomiast asymptota pionowa jest zależna od dziedziny (argument nie należący do dziedziny) i ma postać x=-d/c.
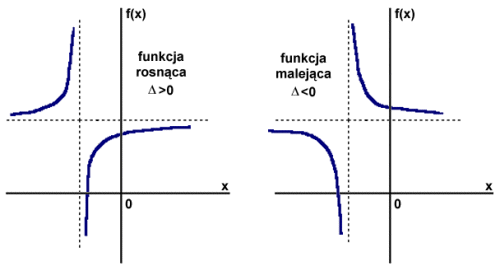
Funkcja homograficzna może być na całej swojej długości (poza punktem x=-d/c - asymptotą pionową) malejąca lub rosnąca. Przy określaniu tego faktu korzysta się ze znaku wyznacznika D:
- Jeśli D>0 - funkcja jest rosnąca.
- Jeśli D<0 - funkcja jest malejąca.
Najbardziej podstawową funkcją homograficzną jest funkcja o równaniu
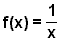
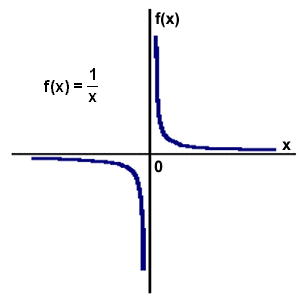
Funkcja ta wygląda następująco: