Funkcje trygonometryczne

Funkcje trygonometryczne.

Funkcje trygonometryczne liczby rzeczywistej.

Funkcje trygonometryczne liczby rzeczywistej, są to funkcje sinus (sin), cosinus (cos), tangens (tg) i cotangens (ctg) określone następująco: jeśli dla pewnej liczby całkowitej k liczba $x-2k\pi$ jest miarą łukową kąta skierowanego $\alpha$ , to $\sin x=\sin\alpha,\ \cos x=\cos\alpha,\ tg x=tg\alpha,\ ctg x=ctg\alpha$ .

Funkcja sinus.

Funkcja sinus jest funkcją określoną w całej dziedzinie, okresową - okres tej funkcji wynosi 2p. Przyjmuje wartości od -1 do +1. Wykresem funkcji sinus jest krzywa zwana sinusoidą.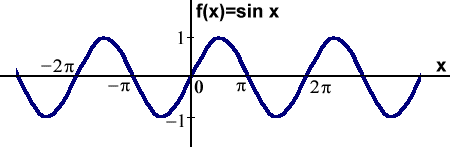

Funkcja cosinus.

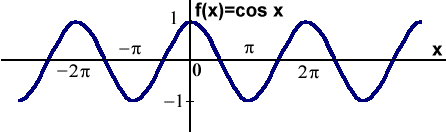
Funkcja cosinus jest funkcją określoną w całej dziedzinie, okresową - okres tej funkcji wynosi 2p. Jest przesunięta względem funkcji sinus o kąt $\frac{\pi}{2}$ ( $\cos x=\sin\left(x+\frac{\pi}{2}\right)$ ). Przyjmuje wartości od -1 do +1. Wykresem funkcji cosinus jest krzywa zwana cosinusoidą.

Funkcja tangens.

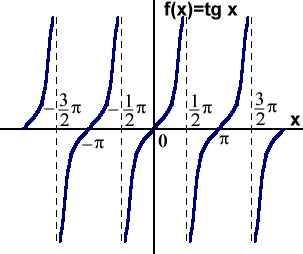
Funkcja tangens jest jest określona, nieparzysta i ciągła w zbiorze powstałym ze zbioru wszystkich liczb rzeczywistych przez usunięcie liczb mających postać $(2k-1)\frac{\pi}{2}$ , gdzie k jest liczbą całkowitą, przybiera wszystkie wartości rzeczywiste, jest okresowa o okresie podstawowym $\pi$ - jej wykresem jest krzywa zwana tangensoidą.

Funkcja cotangens.

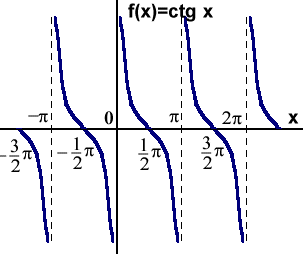
Funkcja cotangens jest funkcją nieokreśloną w punktach kp, okresową - okres tej funkcji wynosi p. Przyjmuje wszystkie wartości ze zbioru liczb rzeczywistych. Jest odwrotnością funkcji tangens - $ctg\ x=\frac{1}{tg\ x}$ . Wykresem funkcji cotangens jest krzywa zwana cotangensoidą.

Wzory zależności pomiędziy funkcjami trygonometrycznymi.

Dla dowolnej liczby rzeczywistej x zachodzą związki:

$\sin x=\sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}$ ;

$\cos x=\sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n}}{(2n)!}$ .

Między funkcjami trygonometrycznymi liczby rzeczywistej tego samego argumentu zachodzą następujące związki:

$\sin^{2}x+\cos^{2}x=1$ ;

$\frac{\sin x}{\cos x}=tg x$ ;

$\frac{\cos x}{\sin x}=ctg x$ .

Korzystając z tych związków można każdą funkcję trygonometryczną liczby rzeczywistej wyrazić za pomocą innej funkcji trygonometrycznej tego samego argumentu:

$\sin^{2}x=1-\cos^{2}x=\frac{tg^{2}x}{1+tg^{2}x}=\frac{1}{1+ctg^{2}x}$ ;

$\cos^{2}x=1-\sin^{2}x=\frac{1}{1+tg^{2}x}=\frac{ctg^{2}x}{1+ctg^{2}x}$ ;

Sumy i różnice funkcji trygonometrycznych są określone wzorami:

$\sin x+\sin y=2\sin\frac{1}{2}(x+y)\cos\frac{1}{2}(x-y)$ ;

$\sin x-\sin y=2\cos\frac{1}{2}(x+y)\sin\frac{1}{2}(x-y)$ ;

$\cos x+\cos y=2\cos\frac{1}{2}(x-y)\cos\frac{1}{2}(x-y)$ ;

$\cos x-\cos y=-2\sin\frac{1}{2}(x+y)\sin\frac{1}{2}(x-y)=2\sin\frac{1}{2}(x+y)\sin\frac{1}{2}(y-x)$ ;

$tg x\pm tg y=\frac{\sin(x\pm y)}{\cos x\cos y}$ ;

$ctg x\pm ctg y=\frac{\sin(y\pm x)}{\sin x\sin y}$ .

Funkcje trygonometryczne liczby rzeczywistej połowy argumentu wyrażają zależności:

$\sin^{2}\frac{1}{2}x=\frac{1-\cos x}{2}$ ;

$\cos^{2}\frac{1}{2}x=\frac{1+\cos x}{2}$ ;

$tg^{2}\frac{1}{2}x=\frac{1-\cos x}{1+\cos x}$ ;

$ctg^{2}\frac{1}{2}x=\frac{1+\cos x}{1-\cos x}$ ;

$tg\frac{1}{2}x=\frac{1-\cos x}{\sin x}=\frac{\sin x}{1+\cos x}$ ;

$ctg\frac{1}{2}x=\frac{1+\cos x}{\sin x}=\frac{\sin x}{1-\cos x}$ .

Funkcje trygonometryczne liczby rzeczywistej sum i różnic argimentów są określone wzorami:

$\sin(x\pm y)=\sin x\cos y\pm\cos x\sin y$ ;

$\cos(x\pm y)=\cos x\cos y\mp\sin x\sin y$ ;

$tg(x\pm y)=\frac{tg x\pm tg y}{1\mp tg x\ tg y}$ ;

$ctg(x\pm y)=\frac{ctg x\ ctg x\mp 1}{ctg x\pm ctg y}$ .

Funkcje trygonometryczne liczby rzeczywistej wielokrotności srgumentów określają wzory:

$\sin 2x=2\sin x\cos x$ ;

$\cos 2x=\cos^{2}x-\sin^{2}x=2\cos^{2}x-1=1-2\sin^{2}x$ ;

$tg2x=\frac{2tgx}{1-tg^{2}x}$ ;

$ctg2x=\frac{ctg^{2}x-1}{2ctgx}$ ;

$\sin 3x=3\sin x-4\sin^{3}x$ ;

$\cos 3x=4\cos^{3}x-3\cos x$ ;

$tg3x=\frac{3tgx-tg^{3}x}{1-3tg^{2}x}$ ;

$ctg3x=\frac{ctg^{3}x-3ctgx}{3ctg^{2}x-1}$ .

Secans i cosecans.

Oprócz czterech podstawowych funkcji trygonometrycznych rozważa się jeszcze dwie funkcje secans i cosecans. Obecnie jednak używane bardzie rzadko. Funkcja secans została wprowadzona przez m.Kopernika w dziele De revolutionibus.

$secx=\frac{1}{\cos x}, cosecx=\frac{1}{\sin x}$

Dodaj komentarz

JComments

matematyka.net

Polski Portal Matematyczny

Menu