Funkcja logarytmiczna
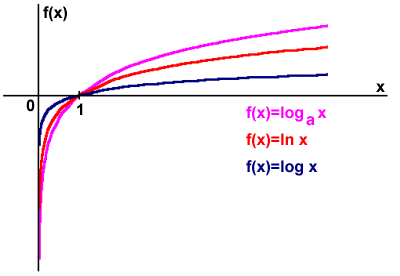
Funkcja logarytmiczna jest to funkcja typu f(x)=logax, przy czym podstawa logarytmu a jest ustaloną liczbą dodatnią różną od zera. Dziedziną funkcji logarytmicznej jest zbiór liczb rzeczywistych dodatnich, a przeciwdziedziną (wartości funkcji) jest zbiór liczb rzeczywistych. Funkcja logarytmiczna posiada jedno miejsce zerowe, które to jest niezależne od wartości podstawy a i wynosi xo=1. W zależności od podstawy logarytmu funkcję logarytmiczną można podzielić na dwie grupy:
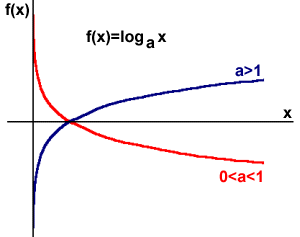
- 0<a<1 - funkcja jest malejąca
- a>1 - funkcja jest rosnąca
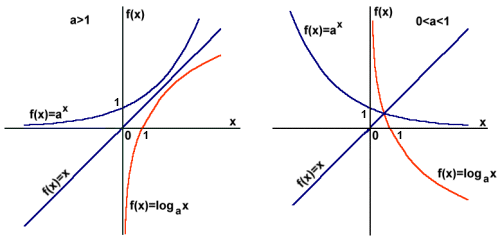
Funkcja logarytmiczna f(x)=logax jest funkcją odwrotną do funkcji wykładniczej f(x)=ax. Wykresy tych funkcji są symetryczne względem prostej f(x)=x.
Wiadomo, że w zależności od podstawy istnieją trzy grupy logarytmów: