Graniastosłupy.
Graniastosłup to wielościan, którego wszystkie wierzchołki leżą na dwóch różnych płaszczyznach równoległych, a krawędzie nie zawarte w tych płaszczyznach są równoległe. Płaszczyzny równoległe zawierające wierzchołki graniastosłupa nazywają się płaszczyznami podstaw graniastosłupa. Część wspólna graniastosłupa z każdą z tych płaszczyzn jest jego ścianą - ściany te nazywają się podstawami graniastosłupa. Obie podstawy graniastosłupa przystają do siebie. Boki podstaw graniastosłupa nazywają się krawędziami podstaw graniastosłupa, a pozostałe krawędzie - krawędziami bocznymi graniastosłupa. Każdy odcinek (również jego długość) o końcach leżących na płaszczyznach podstaw graniastosłupa i prostopadły do tych płaszczyzn nazywa się wysokością graniastosłupa. Jeśli krawędzie boczne graniastosłupa są prostopadłe do płaszczyzny podstaw, to taki graniastosłup nazywa się graniastosłupem prostym. Jeśli krawędzie boczne nie są prostopadłe, to graniastosłup nazywa się graniastosłupem pochyłym. Graniastosłup, którego podstawa jest n-kątem, nazywa się graniastosłupem n-kątnym. Graniastosłup prosty, którego podstawą jest wielokąt foremny, nazywa się graniastosłupem prawidłowym. Objętość graniastosłupa jest równa s*h, gdzie s jest polem podstawy graniastosłupa, h - jego wysokością. Przekrojem poprzecznym graniastosłupa nazywa się część wspólną graniastosłupa z płaszczyzną przecinającą wszystkie jego krawędzie boczne. Przekrojem przekątnym graniastosłupa nazywa się część wspólną tego graniastosłupa z płaszczyzną przechodzącą przez jego dwie krawędzie nie należące do jednej ściany. Jeśli płaszczyzna nierównoległa do płaszczyzny podstawy graniastosłupa ma niepustą część wspólną z graniastosłupem, ale nie przecina jego podstaw, to dzieli ona graniastosłup na dwa wielościany, z których każdy nazywa się graniastosłupem ściętym. Podstawami graniastosłupa ściętego są: podstawa przecinanego graniastosłupa i część wspólna graniastosłupa z płaszczyzną przecinającą. Graniastosłup nazywa się graniastosłupem wpisanym w walec, jeśli jego podstawy są wielokątami wpisanymi w podstawy walca. Graniastosłup nazywa się graniastosłupem opisanym na walcu, jeśli jego podstawy są wielokątami opisanymi na podstawach walca.
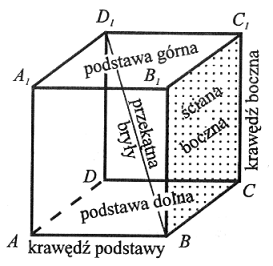 |
Wysokość graniastosłupa jest to odcinek prostopadły do podstaw i zawarty między obydwoma podstawami. Przekątna graniastosłupa jest to odcinek łączący dwa wierzchołki nie leżące na jednej ścianie (np.: BD1). |
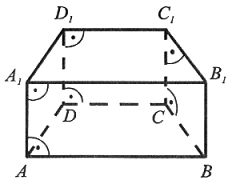
Wśród graniastosłupów wyróżniamy:
 |
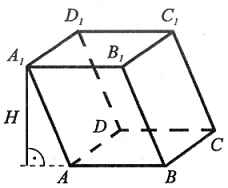
Krawędzie boczne graniastosłupów prostych są prostopadłe do obydwóch podstaw, np.: AA1 ⊥ AB i AA1 ⊥ A1B1; CC1 ⊥ DC i CC1 ⊥ D1C1 |
 |
Podstawy graniastosłupów pochyłych są równoległe, a krawędzie boczne nie są prostopadłe do podstaw. |
Ze względu na kształt podstawy wyróżniamy graniastosłupy: trójkątne, czworokątne, pięciokątne itd.
| Graniastosłupem prawidłowym nazywamy taki graniastosłup, którego podstawą jest wielokąt foremny (trójkąt równoboczny, kwadrat, pięciokąt foremny, sześciokąt foremny,...). |
Prostopadłościan
| Prostopadłościanem nazywamy graniastosłup prosty, którego wszystkie ściany są prostokątami. |
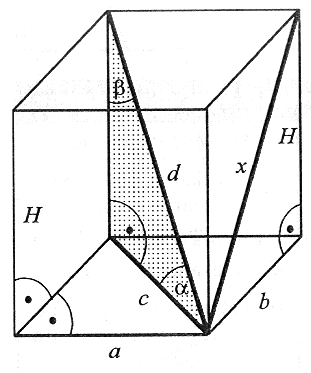 |
a, b - krawędź podstawy, H - wysokość prostopadłościanu (krawędź boczna), c - przekątna podstawy, x - przekątna ściany bocznej, d - przekątna prostopadłościanu, α - kąt nachylenia przekątnej prostopadłościanu do podstawy, β - kąt między krawędzią boczną (wysokością) i przekątną prostopadłościanu. |
Pc = 2ab + 2aH + 2bH |
||
V = a · b · H |
||
Sześcian
| Sześcianem nazywamy prostopadłościan, który ma wszystkie krawędzie równej długości. Jego wszystkie ściany są kwadratami. |
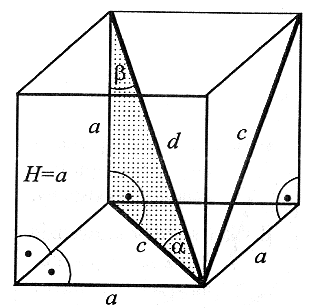 |
a - krawędź sześcianu, c - przekątna podstawy i ściany bocznej (w sześcianie są równe), d - przekątna sześcianu, α - kąt nachylenia przekątnej sześcianu do podstawy, β - kąt między krawędzią boczną i przekątną sześcianu. |
Sześcian jest szczególnym przypadkiem prostopadłościanu.
Pc = 6a2 |
||
V = a3 |
||
Graniastosłup prawidłowy trójkątny
| Graniastosłupem prawidłowym trójkątnym nazywamy graniastosłup, którego podstawą jest trójkąt równoboczny, a jego ściany boczne są przystającymi (równymi) prostokątami. | 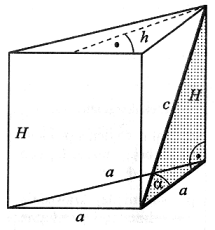 |
a - krawędź podstawy, H - wysokość graniastosłupa, h - wysokość podstawy, c - przekątna ściany bocznej, α - kąt nachylenia przekątnej ściany bocznej do krawędzi podstawy. |
|
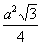 |
Pc = 2 · 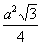 + 3a · H + 3a · H |
|
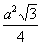 · H · H |
||
Graniastosłup prawidłowy czworokątny
| Graniastosłupem prawidłowym czworokątnym nazywamy graniastosłup, którego podstawą jest kwadrat, a jego ściany boczne są przystającymi (równymi) prostokątami. | 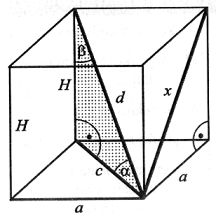 |
a - krawędź podstawy, H - wysokość graniastosłupa, c - przekątna podstawy, d - przekątna graniastosłupa, x - przekątna ściany bocznej α - kąt nachylenia przekątnej graniastosłupa do podstawy, β - kąt pomiędzy krawędzią boczną i przekątną graniastosłupa. |
|
Pc = 2a2 + 4a · H |
||
Komentarze
Kanał RSS z komentarzami do tego postu.