Trójkąty jako figury geometryczne płaskie i ich najważniejsze elementy.
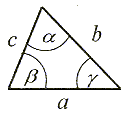
Trójkątem nazywamy domkniętą i ograniczoną część płaszczyzny ograniczoną łamaną zwyczajną zamkniętą o trzech bokach - wielokąt o trzech bokach. Jeden z boków, dowolnie wyróżniony, nazywa się podstawą trójkąta, dwa pozostałe ramionami trójkąta. Trójkąt o równych ramionach nazywa się trójkątem równoramiennym. Jeżeli wszystkie boki trójkąta są równe, trójkąt nazywa się trójkątem równobocznym. Boki trójkąta spełniają tzw. warunek trójkąta, tzn. długość dowolnego z nich jest mniejsza od sumy długości boków pozostałych. Liczba równa sumie długości boków trójkąta nazywa się obwodem trójkąta. Kąt wypukły o ramionach zawierających dwa boki trójkąta (również jego miara) nazywa się kątem wewnętrznym trójkąta lub kątem trójkąta. W trójkącie równoramiennym kąty wewnętrzne przy podstawie trójkąta są równe. Jeżeli wszystkie kąty wewnętrzne danego trójkąta są ostre, to trójkąt nazywa się trójkątem ostrokątnym, jeżeli jeden z jego kątów wewnętrznych jest rozwarty - trójkątem rozwartokątnym; jeżeli jeden z kątów wewnętrznych trójkąta jest prosty - trójkątem prostokątnym. Kątem zewnętrznym trójkąta jest kąt przyległy do kąta wewnętrznego trójkąta. Suma miar kątów trójkąta jest równa mierze kąta półpełnego π (180°). Boki i kąty wewnętrzne trójkąta nazywa się elementami trójkąta. Punkt wspólny dwóch boków trójkąta nazywa się wierzchołkiem trójkąta. Trójkąt jest najmniejszą figurą geometryczną wypukłą zawierającą swoje wierzchołki, jest więc dwuwymiarowym sympleksem. Wierzchołek trójkąta i nie zawierający go bok trójkąta nazywa się przeciwległymi. Trójkąt o wierzchołkach A, B, C oznacza się symbolem ΔABC. Odcinek łączący środek boku trójkąta z wierzchołkiem mu przeciwległym nazywa się środkową trójkąta. Środkowe trójkąta przecinają się w jednym punkcie, który dzieli każdą z nich w stosunku 1:2. Punkt przecięcia środkowych trójkąta jest środkiem ciężkości trójkąta.
 |
Suma miar kątów wewnętrznych trójkąta jest równa 180°. α + β + δ = 180°. |
Każdy bok trójkąta jest mniejszy od sumy dwóch pozostałych boków tego trójkąta.
|AB| < |AC| + |BC|, |AC| < |AB| + |BC| i |BC| < |AB| + |AC|
Wysokości trójkąta
Wysokością trójkąta nazywamu odcinek poprowadzony z wierzchołka trójkąta prostopadle do przeciwległego boku lub do przedłużenia tego boku.
Każdy trójkąt ma trzy wysokości, które przecinają sie w jednym punkcie zwanym ortocentrum (p.O).
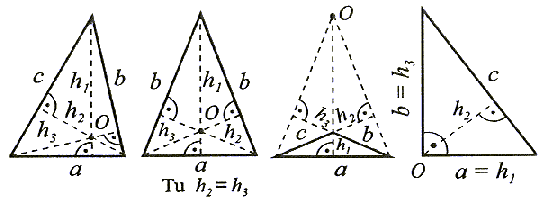
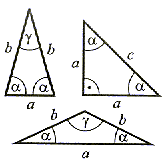
Środkowe boków trójkąta
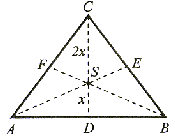 |DS| =  |CD|, |ES| = |CD|, |ES| =  |AE| |AE|oraz |FS| =  |BF| |BF| |
Środkową boku trójkąta nazywamy odcinkiem łączącym środek tego boku z przeciwległym bokiem tego trójkąta. Każdy trójkąt ma trzy srodkowe przecinające się w jednym punkcie (p.S), który nazywamy środkiem ciężkości tego trójkąta. |
Punkt S (środek ciężkości) dzieli każdą środkową w stosunku 1:2, czyli:
|DS| =  |CS|, |ES| =
|CS|, |ES| =  |AS| oraz |FS| =
|AS| oraz |FS| =  |BS|.
|BS|.
Odcinki łączące środki boków trójkąta
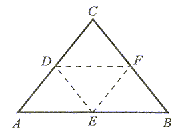 |
Odcinki łączące środki boków trójkąta są równoległe do przeciwległych boków i równe ich połowie. |
DF||AB i |DF| =  |AB|, EF||AC i |EF| =
|AB|, EF||AC i |EF| =  |AC| oraz DE||BC i |DE| =
|AC| oraz DE||BC i |DE| =  |BC|
|BC|
Dwusieczne kątów trójkąta
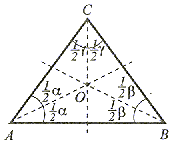 |
Dwusieczna kąta jest to półprosta dzieląca kąt na połowy. Każdy trójkąt ma trzy dwusieczne przecinające się w jednym punkcie (p.O), który jest środkiem koła wpisanego w trójkąt. |
Symetralne boków trójkąta
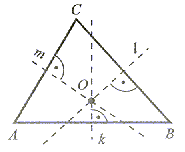 |
Symetralną boku trójkąta nazywamy prostą prostopadłą do tego boku, przechodzącą przez jego środek. Każdy trójkąt ma trzy symetralne boków, przecinające się w jednym punkcie (p.O), który jest środkiem koła opisanego na tym trójkącie |
Środek O koła opisanego na trójkącie może leżeć wewnątrz lub na zewnątrz trójkąta, a w przypadku trójkąta prostokątngo na jego goku (w połowie przeciwprostokątnej).
Trójkąty nie mają środka symetrii.
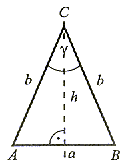 |
Trójkąt równoramienny ma jedną oś symetrii i jest ona jednocześnie dwusieczną kąta (δ) zawartego między ramionami oraz pokrywa się z wysokością figury, symetralną i środkową podstawy. |
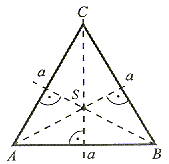 |
Trójkąt równoboczny ma trzy osie symetrii, które są jednocześnie dwusiecznymi kątów, wysokościami, symetralnymi i środkowymi boków figury. |
Punkt przecięcia (C) osi symetrii jest środkiem koła wpisanego i opisanego na trójkącie równobocznym.
Rodzaje trójkątów.
(dowolny) 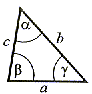 Każdy bok ma inną długość i każdy kąt ma inną miarę. |
 Ma dwa boki równe i nazywamy je ramionami. Trzeci bok to podstawa. Kąty przy podstawie mają tę samą miarę. |
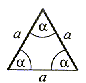 Ma wszystkie boki równej długości. Wszystkie kąty wewnętrzne są równe i mają po 60°. |
(dowolny) 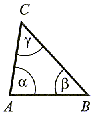 β < 90° δ < 90° Każdy kąt wewnętrzny jest kątem ostrym. |
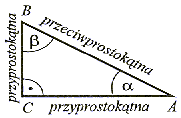 Ma jeden kąt prosty, a dwa pozostałe są ostre i takie, że α + β = 90° |
 β > 90° δ < 90° Ma jeden kąt rozwarty, a dwa pozostałe są ostre. |
Podział trójkątów ze względu na boki i kąty.
|
ostrokątny |
prostokątny |
rozwartokątny |
|
|
równoboczny (dowolny) |
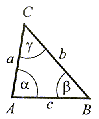 α < 90° β < 90° δ < 90° |
  C = 90° C = 90°α + β = 90° |
 90° < α < 180° α < 90° i β < 90° |
|
równoramienny |
 α = β, α < 90° β < 90°, δ < 90° |
 α = β = 45° 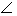 C = 90° C = 90° |
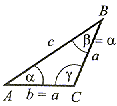 α = β, α < 90° β < 90° 90° < δ < 180° |
|
równoboczny |
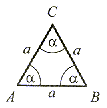 α = 60° |
takiego trójkąta |
takiego trójkąta |
Cechy przystawania trójkątów.
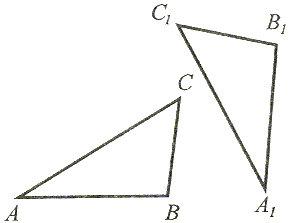 |
Jeżeli boki jednego trójkąta są przystające (równe) do odpowiednich boków drugiego trójkąta, to te trójkąty są przystające. |
|AB| = |A1B1|, |BC| = |B1C1| oraz |AC| = |A1C1|, to  ABC
ABC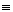
 A1B1C1
A1B1C1
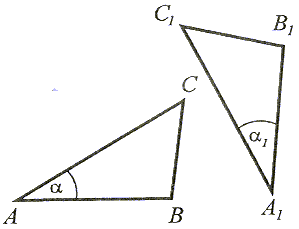 |
Jeżeli dwa boki i kąt między nimi zawarty jednego trójkąta są przystające (równe) do odpowiednich boków i kąta zawartego między nimi w drugim trójkącie, to te trójkąty są przystające. |
|AB| = |A1B1|, |AC| = |A1C1| i α = α1, to  ABC
ABC
 A1B1C1
A1B1C1
 |
Jeżeli bok i dwa kąty do niego przyległe jednego trójkąta są przystające (równe) do odpowiedniego boku i kątów do niego przyległych w drugim trójkącie, to te trójkąty są przystające. |
|AB| = |A1B1|, α = α1 oraz β = β1, to  ABC
ABC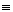
 A1B1C1
A1B1C1
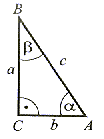
Cechy przystawania trójkątów prostokątnych.
I cecha - Przyprostokątne jednego trójkąta są odpowiednio równe (przystające) przyprostokątnym drugiego trójkąta.
II cecha - Przyprostokątna i kąt ostry do niej przeciwległy jednego trójkąta są odpowiednio równe przyprostokątnej i kątowi do niej przyległemu w drugim trójkącie.
III cecha - Przyprostokątna i kąt do niej przeciwległy jednego trójkąta są odpowiednio równe przyprostokątnej i kątowi do niej przyległemu w drugim trójkącie.
IV cecha -Przeciwprostokątna i jeden z kątów ostrych jednego trójkąta są odpowiednio równe przeciwprostokątnej i jednemu z kątów ostrych w drugim trójkącie.
V cecha -Przeciwprostokątna i jedna z przyprostokątnych jednego trójkąta są odpowiednio równe przeciwprostokątnej i jednej z przyprostokątnych w drugim trójkącie.
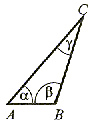
Cechy podobieństwa trójkątów.
Własność, która pozwala na określenie podobieństwa pewnej rodziny figur, nazywa się cechą podobieństwa figur tej rodziny.
Wyróżniamy trzy cechy podobieństwa trójkątów:
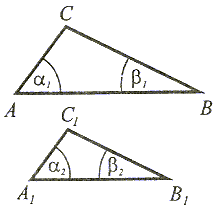 α1 = α2 oraz β1 = β2 |
Jeżeli dwa kąty jednego trójkąta są przystające do odpowiednich kątów drugiego trójkąta, to trójkąty te są podobne. |
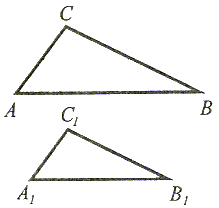 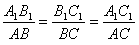 |
Jeżeli stosunki wszystkich boków jednego trójkąta do odpowiednich boków drugiego trójkąta są równe, to trójkąty są podobne. |
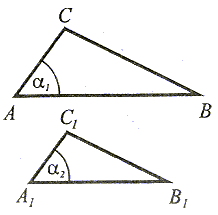 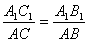 oraz α1 = α |
Jeżeli stosunki dwóch boków jednego trójkąta do odpowiednich boków drugiego trójkąta są równe oraz kąty zawarte między tymi bokami są przystające (równe), to trójkąty te są podobne. |
Cechy podobieństwa trójkątów prostokątnych.
 α1 = α lub β1 = β |
Jeżeli dwa trójkąty prostokątne mają po jednym kącie ostrym przystającym, to te trójkąty są przystające. |
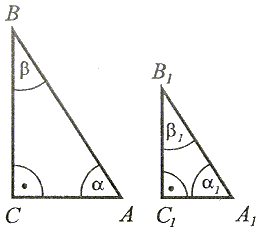
 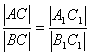 |
Jeżeli stosunek długości przyprostokątnych jednego trójkąta jest równy stosunkowi długości przyprostokątnych drugiego trójkąta, to te trójkąty są podobne. |
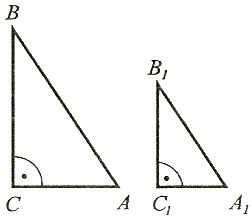 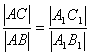 |
Jeżeli stosunek długości przyprostokątnej do długości przeciwprostokątnej jednego trójkąta jest równy stosunkowi odpowiedniej przyprostokątnej do przeciwprostokątnej drugiego trójkąta, to te trójkąty są podobne. |
Można też rozpatrywać stosunki przeciwprostokątnych do odpowiednich przyprostokątnych.
Obwód trójkąta.
|
różnoboczny |
równoranienny |
równoboczny |
 |
 |
 |
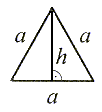
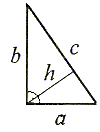
Pole trójkąta.
|
|
|
|
|
|
|
P = |
P = |
P = |
P = |
P = |
Twierdzenie Pitagorasa.
 |
Jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. |
Twierdzenie odwrotne do twierdzenia Pitagorasa.
Jeżeli w trójkącie o bokach długości a, b i c zachodzi równość a2 + b2 = c2, to trójkąt jest prostokątny.
Okrąg opisany na trójkącie.
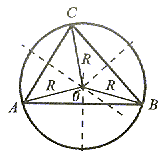 |
Na każdym trójkącie można opisać okrąg. Środkiem okręgu opisanego jest punkt przecięcia się symetralnych boków trójkąta. |
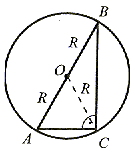 |
Środek okręgu opisanego na trójkącie prostokątnym leży w połowie przeciwprostokątnej. |
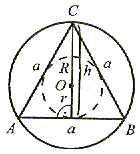 |
Środek okręgu opisanego na trójkącie równobocznym i środek okręgu wpisanegow trójkąt równoboczny pokrywają się. |
Promień okręgu opisanego jest: R = 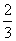 h.
h.
Promień okręgu wpisanego jest: r =  h.
h.
Zależność między obydwoma promieniami: R = 2r.
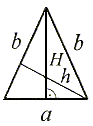
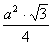
Komentarze
"Środkową boku trójkąta nazywamy odcinkiem łączącym środek tego boku z przeciwległym bokiem tego trójkąta. Każdy trójkąt ma trzy srodkowe przecinające się w jednym punkcie (p.S), który nazywamy środkiem ciężkości tego trójkąta."
Powinno być:
Środkową boku trójkąta nazywamy odcinek łączący środek tego boku z przeciwległym wierzchołkiem tego trójkąta. Każdy trójkąt ma trzy środkowe przecinające się w jednym punkcie (p.S), który nazywamy środkiem ciężkości tego trójkąta.
Czy można ustalić kiedy zastosowano oznaczenie kąta prostego kropką w łuku. Znalazłem takie oznaczenia na kamieniach i zastanawiam się kiedy mogły być wykonane. Są to dwie strzałki rozchodzące się pod kątem prostym i wspomniana kropka w łuku.
Pozdrawiam
Witold
bardzo przydatne informacje!
na szybko - jeden błąd- w: Podział trójkątów ze względu na boki i kąty.- trójkąt różnoboczny(dowolny)
Kanał RSS z komentarzami do tego postu.