Tales z Miletu

Tales z Miletu (640-546 p.n.e.) jest pierwszym znanym z nazwiska greckim mędrcem. O jego życiu wiemy niewiele. Starożytni pisarze nazwali go "pierwszym" filozofem, fizykiem, matematykiem, astronomem. Wyrósł w bujnej atmosferze życia małoazjatyckich kolonii, w których element grecki odgrywał rolę pośrednika w handlu między Wschodem a Grecją właściwą, następnie zaś między Wschodem a Zachodem. Z kontaktów handlowych wywodzi się zapewne i oddziaływanie kultury babilońskiej i egipskiej na małoazjatyckich Greków.
Platon wspomina, że gdy Tales obserwował gwiazdy, wpadł do studni i piękna niewolnica miała się wyrazić żartem, iż chciał zobaczyć, co się dzieje na niebie, a nie dostrzegł, co znajduje się pod jego nogami. Anegdota ta jednak nie charakteryzuje postawy Talesa. Nie był on oderwanym od życia myślicielem, lecz człowiekiem nad wyraz praktycznym, który umiał wykorzystać posiadaną wiedzę w swoich transakcjach handlowych.
Proklos, komentator pierwszej księgi Elementów Euklidesa w oparciu o zaginioną Historię geometrii Euklidesa, przypisuje Talesowi autorstwo następujących twierdzeń geometrycznych:
- Dowód, że średnica dzieli koło na połowy.
- Odkrycie, obok szeregu innych twierdzeń, że kąty przypodstawne w trójkącie równoramiennym są równe.
- Twierdzenie o równości kątów wierzchołkowych i o przystawaniu trójkątów o równym boku i przyległych dwu kątach.
 Talesowi przypisuje się również autorstwo twierdzenia, że kąt wpisany w półokrąg jest prosty.
Talesowi przypisuje się również autorstwo twierdzenia, że kąt wpisany w półokrąg jest prosty.
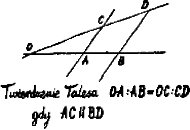
Jego imieniem nazwano twierdzenie o proporcjonalności odcinków, jakie dwie równoległe odcinają na ramionach kąta.
Wymienione twierdzenia nie stanowiły w epoce Talesa żadnej rewolucji wobec poziomu, który osiągnęła zamarła już w owym czasie w rozwoju matematyka egipska i babilońska. Wielkość Talesa jako matematyka polega raczej na tym, że z jego imieniem wiąże się pojęcie dowodu twierdzenia. Matematyków egipskich i babilońskich interesowało pytanie "jak". Tales zaś, o ile wiemy, pierwszy pytał "dlaczego". Nie jesteśmy dziś w stanie ustalić, jak Tales przeprowadził dowód. Wybitny historyk matematyki starogreckiej T.Heath utrzymuje, że tak oczywistego faktu, jak ten, iż średnica dzieli koło na połowy, nie dowodził również Euklides; wszakże Eudemos, pisarz epoki Euklidesa, znał zapewne pojęcie dowodu i nie ma podstaw, aby odrzucić jego relację, iż Tales dowody przeprowadzał.
Talesa można uznać za tego, który łącząc teorię z praktykę zbudował fundamenty geometrii jako nauki dedukcyjnej, której ukoronowaniem były Elementy Euklidesa.