Euklides

Euklides (około 300 r.p.n.e.) Elementy Euklidesa są zapewne najbardziej rozpowszechnionym dziełem naukowym, którego liczba wydań od wynalezienia druku przekracza tysiąc, a wcześniejsze kopie stanowiły jedyny, używany w ówczesnym nauczaniu na odpowiednim poziomie podręcznik geometrii.
Dzieło to składa się z trzynastu ksiąg. Księgi czternasta i piętnasta są późniejszymi uzupełnieniami. Autorem czternastej jest Hipsikles z Aleksandrii (około 200 r.p.n.e.), a piętnastą dołączono dopiero w szóstym wieku naszej ery.
Pierwsze cztery księgi i szósta dotyczą geometrii płaskiej, ostatnie trzy - przestrzennej, których ukoronowaniem są rozważania o pięciu wielościanach foremnych. Piąta poświęcona jest teorii proporcji w ujęciu geometrycznym. Treść księgi siódmej, ósmej i dziewiątej jest arytmetyczna. Autor wykłada w nich arytmetykę pitagorejską, a więc właściwie teorię liczb, lecz w sposób naukowy, bez cienia pitagorejskiej mistyki. Wreszcie w dziesiątej księdze zawarty jest wykład o niewymiernościach, będący spadkiem po Teodorasie z Cyreny i Teartemosie z Aten.
Gdyby porównać treść Elementów z tym, co wiedzieli w zakresie matematyki poprzednicy Euklidesa, nie znaleźlibyśmy, być może, w tym dziele nic nowego, tym bardziej że podobne do Elementów prace istniały wcześniej, choć znamy je tylko z tytułów i nazwisk autorów. Do Euklidesa śmiało można odnieść słowa Pascala: "Niech nikt nie twierdzi, że nie powiedziałem nic nowego; rozmieszczenie treści jest nowe."
Bo istotne, to nowe rozmieszczenie treści olśniewa najbardziej wymagających uczonych do dnia dzisiejszego. W dziele swoim urzeczywistnił Euklides wzór nauki dedukcyjnej, której twierdzenia, jeśli pominąć nieznaczne usterki, wyprowadzane są na drodze czysto logicznej z układu określeń, postulatów i aksjomatów.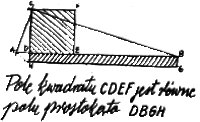

Najbardziej znanym twierdzeniem, nazwanym twierdzeniem Euklidesa jest następujące: "Pole kwadratu zbudowanego na wysokości trójkąta prostokątnego poprowadzonej z wierzchołka kąta prostego jest równe polu prostokąta o bokach równym odcinkom, na które ta wysokość podzieliła przeciwprostokątną". O autorze Elementów wiemy niewiele i nic pewnego. Pisano wiele o jego dziełach, nic o osobie. Życie jego przypada na panowanie Ptolemeusza I (323-283), a więc na początek okresu hellenistycznego, w którym wprawdzie rozszerzyły się wpływy kultury greckiej, ale ona sama uległa oddziaływaniu mistycznych prądów Wschodu. Patronowanie nauce przez władców w tym okresie, a zwłaszcza Ptolemeuszów, którzy stworzyli w Aleksandrii sprzyjające dla rozwoju nauki warunki, a między innymi założyli imponującą bibliotekę, doprowadziło do bujnego rozkwitu nauki i powstania zawodowej grupy uczonych. Poczet wielkich matematyków tej epoki rozpoczyna właśnie Euklides.
Od Proklosa pochodzi niezbyt pewna, lecz charakteryzująca ówczesną atmosferę informacja, według której Euklides na pytanie Ptolemeusza, czy nie ma prostszej drogi do poznania geometrii niż Elementy, miał dumnie odpowiedzieć, że w geometrii nie istnieje osobna droga królewska.
Wolno również przypuszczać, że Euklides pozostawał pod wpływami filozofii platońskiej, jak twierdzi Proklos. Przemawia za tym między innymi cecha Elementów - skrupulatne, tak charakterystyczne dla Platona i jego zwolenników, omijanie wszelkich zagadnień mających związek z praktyką.
W tym samym duchu utrzymana jest informacja Stobajosa: młodzieniec studiujący geometrię pod kierunkiem Euklidesa miał zadać mistrzowi pytanie, co daje studiowanie geometrii.
W odpowiedzi miał się Euklides zwrócić do swego niewolnika ze słowami "Daj mu trzy obole, ten człowiek chce osiągnąć korzyści z nauki".