Jesteś tutaj: Start

Teoria

analiza matematyczna

Funkcja wymierna

Drukuj | E-mail | Odsłony: 10856

Funkcja wymierna.

Funkcja wymierna to funkcja

$x\mapsto\frac{g(x)}{h(x)}=\frac{a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{0}}{b_{m}x^{m}+b_{m-1}x^{m-1}+...+b_{0}}$

będąca ilorazem dwóch wielomianów g i h stopni odpowiednio n i m ( $a_{n}\neq 0,\ b_{m}\neq 0)$ .

Dodaj komentarz

Funkcja charakterystyczna

Drukuj | E-mail | Odsłony: 12108

Funkcja charakterystyczna.

Funkcja charakterystyczna zbioru $Y\subset X$ to funkcja $f: \ X\to \textbf{R}$ określona następująco:

$f(x)=\begin{cases} 1,\ x\in Y,\\ 0,\ x\not\in Y.\end{cases}$

Funkcję charakterystyczną oznacza się też $\chi_{Y}$ lub 1_Y. Funkcje charakterystyczne są często stosowane w teorii miary i całki Lebesgue'a. Przykładem funkcji charakterystycznej jest funkcja Dirichleta.

Funkcja Dirichleta.

Funkcja Dirichleta to funkcja określona następująco:

$f(x)=\begin{cases} 1, dla\ x\ wymiernych,\\ 0, dla\ x\ niewymiernych.\end{cases}$

Funkcja Dirichleta oznacza się często przez $\chi_{Q}$ , jest to funkcja charakterystyczna zbioru liczb wymiernych. Funkcja Dirichleta ma wiele interesujących własności: jest nieciągła w dowolnym punkcie swojej dziedziny, jest okresowa, jej okresami są wszystkie liczby wymierne dodatnie, nie ma okresu zasadniczego, na żadnym przedziale nie jest całkowalna w sensie Riemanna, natomiast na dowolnym podzbiorze $A\subset R$ mierzalnym w sensie Lebesque'a, jest całkowalna w sensie Lebesgue'a i ta całka wynosi zero.

Dodaj komentarz

Wielomiany

Drukuj | E-mail | Odsłony: 26269

Wielomiany

1.Definicja wilomianu - Wilomian jest to funkcja w postaci:

W(x)=a_nxⁿ+a_n-1x^n-1+...+a₂x²+a₁x¹+a₀x⁰

a_kx^k - wyraz stopnia k; a_k - współczynnik wyrazu stopnia k; a₀x⁰ = a₀ - wyraz wolny; n- stopień W(x)
W(x) = 6x⁵ - 2x⁴ + 3x² - x + 7 gdzie: -2x⁴ - wyraz 4 - stopnia; 3 - współczynnik przy x²; 7 - wyraz wolny
W(x) = 6x⁵ - 2x⁴ + 0x³ + 3x² - x + 7 wielomian uzupełniony do pełnego; 5 - stopień wielomianu

2. Równania wielomianowe
Równanie wielomianowe otrzymujemy przyrównując wielomiany do zera.
W(x) = 2x³ - 3x² + 3x - 2 = 0

3. System twierdzeń o miejscach zerowych:
I Twierdzenie o ilości pierwiastków (rozwiązań) równania wielomianowego.
n - parzyste ;W(x) stopnia parzystego może mieć od 0 do n pierwiastków
n - nieparzyste; W(x) stopnia nieparzystego może mieć od 1 do n pierwiastków

II Twierdzenie o rozkładzie wielomianu na czynniki.
Każdy wielomian można rozłożyć na funkcje liniowe i kwadratowe.
W(x) da się rozłożyć na czynniki stopnia pierwszego i drugiego.
Nie znaleziono ogólnej metody na dokonywanie powyższego rozkładu.

4. Metody rozkładania wielomianu na czyniki.
a) Gdy a₀ = 0 to wyłanczamy x przed nawias: 2x³ - 4x² - x = 0 → x(2x² - 4x - 1) = 0 ⇔ x = 0 ∨ 2x² - 4x - 1 = 0
b) Gdy współczynniki są odpowiednio dobrane, rozkładamy przez podwójne wyłączanie przed nawias.
x³ + 3x² - 4x - 12 = 0
x²(x+3) - 4(x+3) = 0
(x+3)(x² - 4 x) = 0 ⇔x + 3 = 0 ∨ x² - 4x=0
c) Rozkład poprzez dziedzlenie. Umożliwia to następujący system twierdzeń.

III Twierdzenie o pierwiastkach całkowitych wielomianu.
Jeżeli wielomian ma pierwiastek całkowity to musi on dzielić wyraz wolny.
x³ - 9x² + 15x - 7 = 0 jeżeli x₀ ∈ C ⇒ x₀ | 7 czyli x₀∈{±1,±7}
Spr. W(1) = 1 - 9 + 15 - 7 = 16 - 16 = 0

IV Twierdzenie o pierwiastkach wymiernych

x₀ ∈ W ⇒ x₀ = n/m ∧ n | a₀ ∧ m | a_n
2x³ - 5x² - 4x + 3 = 0
x₀ ∈ W => x₀ = n/m ∧ n | 3 ∧ m | 2 => x₀ ∈ {±&u1-2;;±1&u1-2;}

V Twierdzenie o podziale wielomianów - Tw.Bezou
W(x₀) = 0 ⇔ (x-x₀) | W(x)
x₀ jest pierwiastkiem wielomianu ⇔ gdy wielomian jest podzielny przez (x-x₀)
W(x) = 2x³ - 5x -4x + 3; x₀ ∈ { ±1;±3}-III Tw.
W(3) = 2*27 - 5*9 - 12 + 3 = 54 - 45 -12 + 3 = 57 - 57 = 0
dzielnik W(x) to (x-3), po przeprowadzeniu dzielenia wynik jest równy 2x² + x - 1
W(x) = (x - 3)*(2x² + x -1) = 0 ⇔ (x-3) = 0 ∨ (2x²+ x - 1) = 0

5.NIerówności wielomianowe

a) Aby rozwiązać nierówność W(x)≥ 0 rozwiązujemy najpierw równanie:
W(x) = 0

b) Rozkładamy zatem wielomiany na czynniki liniowe i kwadratowe W(x) = W¹ * W²...
Znajdujemy wszystkie miejsca zerowe, zwracając uwagę na krotność pierwiastków.
W(x) = (x-2)(x-2)(x² + 5) x₀=2 pierwiastek dwukrotny

c) szkicujemy wykres wielomianu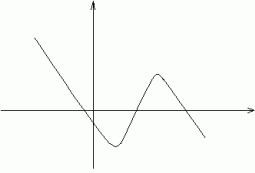

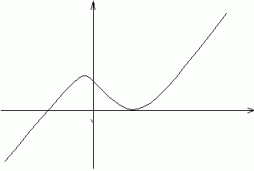
Jest to wykres typu "fala" zależy od stopnia wielomianu.
Przy szkicowaniu bierzemy pod uwagę znak przy najwyższej potędze "x", wykres szkicujemy od prawej strony.
W miejscach zerowych o nieparzystej krotność wielomian zmienia znak!
Niech W(x) = (x-1)(x-2)(x-2)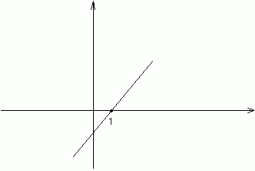

(zmienia znak i przecina oś)
natomiast w miejscu zerowym o parzystej krotności wielomian nie zmienia znaku.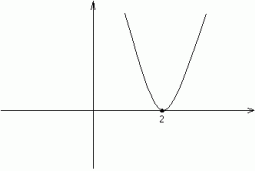

(nie zmienia znaku, dotyka osi - odbija się od osi)

d) zaznaczamy znaki na wykresie.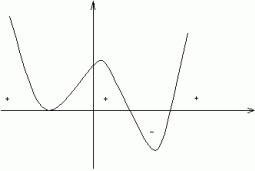

- znaki robimy między wykresem a osią X.
- odczytujemy potrzebne przedziały w których wielomian przybiera odpowiedajace nierówności wartości.

1 komentarz

Funkcja algebraiczna

Drukuj | E-mail | Odsłony: 14823

Funkcja algebraiczna.

Funkcja algebraiczna to funkcja spełniająca równanie algebraiczne - funkcja f, dla której istnieje wielomian niezerowy W dwóch zmiennych taki, że równanie W(x,f(x))=0 jest spełnione dla każdego x należącego do dziedziny funkcji f.Przykładami funkcji algebraicznej są: wielomiany, funkcje wymierne i funkcje niewymierne, tzn. funkcje, których zależność od zmiennej x wyraża się za pomocą działań arytmetycznych i pierwistków, np. $f(x)=x+\sqrt[3]{x-\sqrt{x}}$ . Jeżeli wielomian W dodatniego stopnia względem drugiej zmiennej znika w pewnym punkcie (x₀, y₀) i jego pochodna cząstkowa względem y jest w tym punkcje różna od 0, to istnieje otoczenie x₀ i dokładnie jedna funkcja algebraiczna określona w tym otoczeniu, związana z tym wielomianem. Funkcja ta tylko w wyjątkowych wypadkach wyraża się za pomocą pierwiastków.

Dodaj komentarz

Funkcje trygonometryczne

Drukuj | E-mail | Odsłony: 40222

Funkcje trygonometryczne.

Funkcje trygonometryczne liczby rzeczywistej.

Funkcje trygonometryczne liczby rzeczywistej, są to funkcje sinus (sin), cosinus (cos), tangens (tg) i cotangens (ctg) określone następująco: jeśli dla pewnej liczby całkowitej k liczba $x-2k\pi$ jest miarą łukową kąta skierowanego $\alpha$ , to $\sin x=\sin\alpha,\ \cos x=\cos\alpha,\ tg x=tg\alpha,\ ctg x=ctg\alpha$ .

Funkcja sinus.

Funkcja sinus jest funkcją określoną w całej dziedzinie, okresową - okres tej funkcji wynosi 2p. Przyjmuje wartości od -1 do +1. Wykresem funkcji sinus jest krzywa zwana sinusoidą.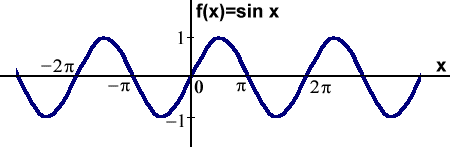

Funkcja cosinus.

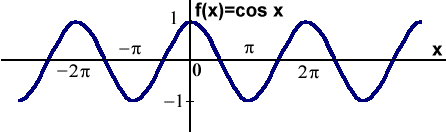
Funkcja cosinus jest funkcją określoną w całej dziedzinie, okresową - okres tej funkcji wynosi 2p. Jest przesunięta względem funkcji sinus o kąt $\frac{\pi}{2}$ ( $\cos x=\sin\left(x+\frac{\pi}{2}\right)$ ). Przyjmuje wartości od -1 do +1. Wykresem funkcji cosinus jest krzywa zwana cosinusoidą.

Funkcja tangens.

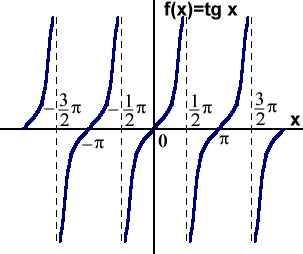
Funkcja tangens jest jest określona, nieparzysta i ciągła w zbiorze powstałym ze zbioru wszystkich liczb rzeczywistych przez usunięcie liczb mających postać $(2k-1)\frac{\pi}{2}$ , gdzie k jest liczbą całkowitą, przybiera wszystkie wartości rzeczywiste, jest okresowa o okresie podstawowym $\pi$ - jej wykresem jest krzywa zwana tangensoidą.

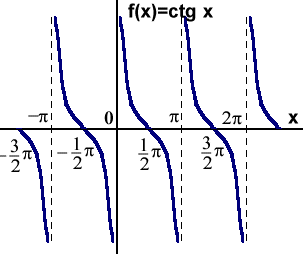
Funkcja cotangens.

Funkcja cotangens jest funkcją nieokreśloną w punktach kp, okresową - okres tej funkcji wynosi p. Przyjmuje wszystkie wartości ze zbioru liczb rzeczywistych. Jest odwrotnością funkcji tangens - $ctg\ x=\frac{1}{tg\ x}$ . Wykresem funkcji cotangens jest krzywa zwana cotangensoidą.

Wzory zależności pomiędziy funkcjami trygonometrycznymi.

Dla dowolnej liczby rzeczywistej x zachodzą związki:

$\sin x=\sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}$ ;

$\cos x=\sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n}}{(2n)!}$ .

Między funkcjami trygonometrycznymi liczby rzeczywistej tego samego argumentu zachodzą następujące związki:

$\sin^{2}x+\cos^{2}x=1$ ;

$\frac{\sin x}{\cos x}=tg x$ ;

$\frac{\cos x}{\sin x}=ctg x$ .

Korzystając z tych związków można każdą funkcję trygonometryczną liczby rzeczywistej wyrazić za pomocą innej funkcji trygonometrycznej tego samego argumentu:

$\sin^{2}x=1-\cos^{2}x=\frac{tg^{2}x}{1+tg^{2}x}=\frac{1}{1+ctg^{2}x}$ ;

$\cos^{2}x=1-\sin^{2}x=\frac{1}{1+tg^{2}x}=\frac{ctg^{2}x}{1+ctg^{2}x}$ ;

Sumy i różnice funkcji trygonometrycznych są określone wzorami:

$\sin x+\sin y=2\sin\frac{1}{2}(x+y)\cos\frac{1}{2}(x-y)$ ;

$\sin x-\sin y=2\cos\frac{1}{2}(x+y)\sin\frac{1}{2}(x-y)$ ;

$\cos x+\cos y=2\cos\frac{1}{2}(x-y)\cos\frac{1}{2}(x-y)$ ;

$\cos x-\cos y=-2\sin\frac{1}{2}(x+y)\sin\frac{1}{2}(x-y)=2\sin\frac{1}{2}(x+y)\sin\frac{1}{2}(y-x)$ ;

$tg x\pm tg y=\frac{\sin(x\pm y)}{\cos x\cos y}$ ;

$ctg x\pm ctg y=\frac{\sin(y\pm x)}{\sin x\sin y}$ .

Funkcje trygonometryczne liczby rzeczywistej połowy argumentu wyrażają zależności:

$\sin^{2}\frac{1}{2}x=\frac{1-\cos x}{2}$ ;

$\cos^{2}\frac{1}{2}x=\frac{1+\cos x}{2}$ ;

$tg^{2}\frac{1}{2}x=\frac{1-\cos x}{1+\cos x}$ ;

$ctg^{2}\frac{1}{2}x=\frac{1+\cos x}{1-\cos x}$ ;

$tg\frac{1}{2}x=\frac{1-\cos x}{\sin x}=\frac{\sin x}{1+\cos x}$ ;

$ctg\frac{1}{2}x=\frac{1+\cos x}{\sin x}=\frac{\sin x}{1-\cos x}$ .

Funkcje trygonometryczne liczby rzeczywistej sum i różnic argimentów są określone wzorami:

$\sin(x\pm y)=\sin x\cos y\pm\cos x\sin y$ ;

$\cos(x\pm y)=\cos x\cos y\mp\sin x\sin y$ ;

$tg(x\pm y)=\frac{tg x\pm tg y}{1\mp tg x\ tg y}$ ;

$ctg(x\pm y)=\frac{ctg x\ ctg x\mp 1}{ctg x\pm ctg y}$ .

Funkcje trygonometryczne liczby rzeczywistej wielokrotności srgumentów określają wzory:

$\sin 2x=2\sin x\cos x$ ;

$\cos 2x=\cos^{2}x-\sin^{2}x=2\cos^{2}x-1=1-2\sin^{2}x$ ;

$tg2x=\frac{2tgx}{1-tg^{2}x}$ ;

$ctg2x=\frac{ctg^{2}x-1}{2ctgx}$ ;

$\sin 3x=3\sin x-4\sin^{3}x$ ;

$\cos 3x=4\cos^{3}x-3\cos x$ ;

$tg3x=\frac{3tgx-tg^{3}x}{1-3tg^{2}x}$ ;

$ctg3x=\frac{ctg^{3}x-3ctgx}{3ctg^{2}x-1}$ .

Secans i cosecans.

Oprócz czterech podstawowych funkcji trygonometrycznych rozważa się jeszcze dwie funkcje secans i cosecans. Obecnie jednak używane bardzie rzadko. Funkcja secans została wprowadzona przez m.Kopernika w dziele De revolutionibus.

$secx=\frac{1}{\cos x}, cosecx=\frac{1}{\sin x}$

Dodaj komentarz

Strona 1 z 2

matematyka.net

Polski Portal Matematyczny

Menu

Funkcja wymierna

Funkcja wymierna.

Funkcja charakterystyczna

Funkcja charakterystyczna.

Funkcja Dirichleta.

Wielomiany

Wielomiany

Funkcja algebraiczna

Funkcja algebraiczna.

Funkcje trygonometryczne

Funkcje trygonometryczne.

Funkcje trygonometryczne liczby rzeczywistej.

Funkcja sinus.

Funkcja cosinus.

Funkcja tangens.

Funkcja cotangens.

Wzory zależności pomiędziy funkcjami trygonometrycznymi.

Secans i cosecans.

Popularne