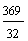Ciąg geometryczny
Ciąg liczbowy nazywamy ciągiem geometrycznym, gdy iloraz dowolnego wyrazu ciągu i wyrazu go poprzedzającego jest stały dla danego ciągu (oznaczamy go przez q).
np. 2, 4, 8, 16, 32, 64, 128
4 : 2 = 2
8 : 4 = 2
16 : 8 = 2 itd.
iloraz wynosi q = 2
Powyższy ciąg jest geometryczny
np. 2, 8, 11, 22, 25, 50
8 : 2 = 4
11 : 8 = 1
22 : 11 = 2 itd.
iloraz nie istnieje
Powyższy ciąg nie jest geometryczny
| Najważniejsze wzory: | |
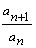 = q = q |
an ≠ 0 |
| an = a1 · qn − 1 | wzór na n-ty wyraz ciągu geometrycznego |
Sn = a1 · 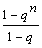 |
q ≠ 1 wzór na sume n początkowych, kolejnych wyrazów ciągu geometrycznego |
S = a1 · 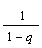 |
|q| < 1 wzór na sume wszystkich wyrazów ciągu geometrycznego |
Przykłady:
Zad. 1
Czy ciąg an = n2 jest geometryczny?
Rozwiązanie:
Należy sprawdzić, czy iloraz 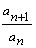 jest stały (jest liczbą).
jest stały (jest liczbą).
| Utwórzymy ten iloraz: | |
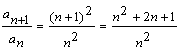 |
korzystamy ze wzoru (x + y)2 = x2 + 2xy + y2 |
Iloraz nie jest stały, zależy od n, zmienia swoją wartość wraz ze zmianą n.
Ciąg an = n2 nie jest geometryczny.
Zad. 2
Wiedząc, że ciąg jest geometryczny i mając dane a1 = 2; q = 1,25; n = 4 znajdź: an; Sn.
Rozwiązanie:
Najpierw znajdujemy an (n-ty wyraz ciągu geometrycznego).
W tym celu posłużymy się wzorem an = a1 · qn−1.
| an = a1 · qn−1 a4 = 2 · (1,25)4 − 1 a4 = 2 · (1,25)3 = 2 · 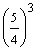 = == 2 · 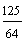 = = 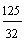 |
do wymienionego wzoru podstawiamy dane z zadania |
Teraz znajdujemy Sn (sumę n początkowych, kolejnych wyrazów ciągu geometrycznego).
W tym celu posłużymy się wzorem Sn = a1 · 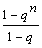
S4 = 2 · 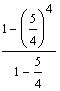 = 2 · = 2 · 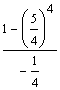 = == 2 · (−4) · (1 − 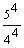 ) = ) == −8 · (1 − 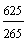 ) = ) == −8 · ( 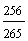 − − 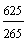 ) = ) == −8 · 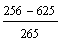 = == − 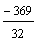 = = 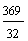 S4 = 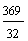 |
do wymienionego wzoru podstawiamy dane z zadania |
Odp. a4 = 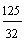 , S4 =
, S4 =