Zbiory liczbowe.
Zbiór liczbowy to zbiór, którego elementem są liczby. Oś liczbowa to prosta, na której ustalono zwrot dodatni, punkt zerowy i jednostkę. |
|
| Zbiór liczb naturalnych - N | N = {0, 1, 2, ...} N+ = {1, 2, 3, ...} - zbiór liczb naturalnych dodatnich |
| Zbiór liczb całkowitych - C | C = {..., −3, −2, −1, 0, 1, 2, 3, ...} C+ = N+ C− = {..., −3, −2, −1} - zbiór liczb całkowitych ujemnych |
| Zbiór liczb wymiernych - W | W = 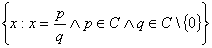 Każdą liczbę wymierną można przedstawic w postaci ułamka dziesiętnego skończonego lub rozwinięcia dziesiętnego nieskończonego okresowego. |
| Zbiór liczb niewymiernych - IW | Liczbą niewymierną nazywamy tę liczbę, która nie jest liczbą wynierną, czyli nie daje się przedstawić w postaci 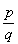 , gdzie , gdziep ∈ C i q ∈ C \ {0}. Rozwinięcie dziesiętne liczby niewymiernej jest nieskończone i nieokresowe. |
| Zbiór liczb rzeczywistych - R | Każdej liczbie rzeczywistej odpowiada na osi liczbowej tylko jeden punkt. Każdemu punktowi na osi liczbowej odpowiada tylko jedna liczba rzeczywista. R = W ∪ IW R = R+ ∪ R− ∪ {0} |
| Związki między zbiorami liczbowymi | 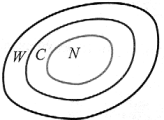  W ∪ IW = R W ∩ IW = Ø N ⊂ C ⊂ W ⊂ R IW ⊂ R |