Relacje między zbiorami.
Zawieranie się zbiorów (inkluzja)
| Zbiór A zawiera się w zbiorze B, jeżeli każdy element zbioru A jest elementem zbioru B.biór A jest nazywany podzbiorem zbioru B i zapisujemy A ⊂ B | 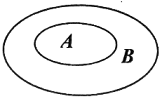 |
Równość zbiorów
| Zbiory A i B są równe , gdy każdy element zbioru A jest elementem zbioru B i każdy element zbioru B jest elementem zbioru A. Równość zbiorów A i B zapisujemy A = B. |
Przykłady równości zbiorów:
Porównajmy dwa zbiory:
Zbiór liter wyrazu matematyka {M, A, T, E, M, A, T, Y, K, A} i zbiór {A, E, K, M, T, Y}.
Wypisując elementy zbioru, musimy pamietać, że każdy element wystarczy zapisać tylko jeden raz. Widzimy więc, że każdy element pierwszego zbioru jest elementem drugiego zbioru oraz każdy element drugiego zbioru jest elementem zbioru pierwszego.
Możemy więc zapisać równość:
{M, A, T, E, M, A, T, Y, K, A} = {A, E, K, M, T, Y}.
Zbiory równoliczne
| Zbiory skończoneA i B są równoliczne , gdy liczba elementów zbioru A jest równa liczbie elementów w zbiorze B i każdy element zbioru B jest elementem zbioru A. Równość zbiorów A i B zapisujemy A = B. |
Przykład:
A = {−3, −2, −1, 0} i B = {0, 1, 2, 3} Zbiory A i B są równoliczne (każdy z nich ma po 4 elementy), ale nie są równe, bo ich elementy są różne.
Zbiory rozłączne
| Zbiory A i B nazywamy rozłącznymi, jeżeli nie mają one żadnych elementów wspólnych czyli, że A ∩ B ∈ Ø | 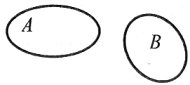 |
Iloczyn kartezjański
Zbiór X 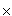 Y nazywamy iloczynem kartezjański, zbiorów X i Y. Y nazywamy iloczynem kartezjański, zbiorów X i Y.X 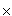 Y = {(x, y): x ∈ X ∧ y ∈ Y}. Y = {(x, y): x ∈ X ∧ y ∈ Y}.X  X = X2. X = X2. |