Moc zbioru.
Moc zbioru, liczba kardynalna, uogólnienie pojęcia liczby elementów zbioru skończonego na dowolne zbiory. Moc zbioru A oznacza się symbolem , #A lub card A. Moc zbioru przyporządkowana jest każdemu zbiorowi w taki sposób, że zbiory równoliczne (tzn. takie, że istnieje funkcja różnowartościowa przekształcająca jeden zbiór na drugi) mają równą moc. Mocą zbiorów skończonych są liczby naturalne, będące liczbami elementów tych zbiorów. Mocą zbiorów, które nie są liczbami naturalnymi, są moce zbiorów nieskończonych (nieskończone liczby kardynalne). Jest ich nieskończenie wiele.
Dodaj komentarz
Przedziały liczbowe (a, b ∈ R i a < b)
| Przedziały ograniczone: przedział otwarty (a; b) ............... (a; b) = {x: x ∈ R i a < x < b} 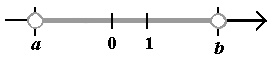 przedział domknięty <a; b> ......... <a; b> = {x: x ∈ R i a ≤ x ≤ b} 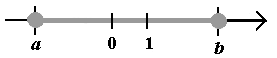 przedział lewostronnie domknięty lub prawostronnie otwarty <a; b) ...... <a; b> = {x: x ∈ R i a ≤ x < b} 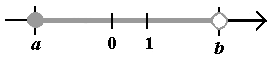 przedział prawostronnie domknięty lub lewostronnie otwarty (a; b> ..........(a; b> = {x: x ∈ R i a < x ≤ b} 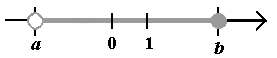 Przedziały nieograniczone: otwarty (−∞; a) ............................... (−∞; a) = {x: x ∈ R i x < b} 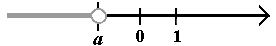 otwarty (a;+∞) ................................. (a;+∞) = {x: x ∈ R i x > b} 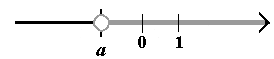 prawostronnie domknięty (−∞; a> .... (−∞; a> = {x: x ∈ R i x ≤ b} 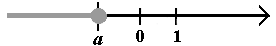 lewostronnie domknięty <a; +∞) ...... <a; +∞) = {x: x ∈ R i x ≥ b} 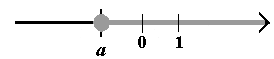 |
Prawa rachunku zbiorów.
| Przemienność sumy zbiorów | A ∪ B = B ∪ A |
| Przemienność iloczynu zbiorów | A ∩ B = B ∩ A |
| Łączność sumy zbiorów | (A ∪ B) ∪ C = A ∪ (B ∪ C) |
| Łączność iloczynu zbiorów | (A ∩ B) ∩ C = A ∩ (B ∩ C) |
| Prawa de Morgana dla zbiorów | (A ∩ B)' = A' ∪ B' (A ∪ B)' = A' ∩ B' |
| Rozdzielność iloczynu względem sumy zbiorów | A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) |
| Rozdzielność iloczynu względem sumy zbiorów | A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) |
| Wnioski z praw rozdzielności | A ∪ (A ∩ B) = A A ∩ (A ∪ B) = A |
Zbiory liczbowe.
Zbiór liczbowy to zbiór, którego elementem są liczby. Oś liczbowa to prosta, na której ustalono zwrot dodatni, punkt zerowy i jednostkę. |
|
| Zbiór liczb naturalnych - N | N = {0, 1, 2, ...} N+ = {1, 2, 3, ...} - zbiór liczb naturalnych dodatnich |
| Zbiór liczb całkowitych - C | C = {..., −3, −2, −1, 0, 1, 2, 3, ...} C+ = N+ C− = {..., −3, −2, −1} - zbiór liczb całkowitych ujemnych |
| Zbiór liczb wymiernych - W | W = 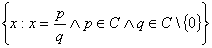 Każdą liczbę wymierną można przedstawic w postaci ułamka dziesiętnego skończonego lub rozwinięcia dziesiętnego nieskończonego okresowego. |
| Zbiór liczb niewymiernych - IW | Liczbą niewymierną nazywamy tę liczbę, która nie jest liczbą wynierną, czyli nie daje się przedstawić w postaci 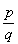 , gdzie , gdziep ∈ C i q ∈ C \ {0}. Rozwinięcie dziesiętne liczby niewymiernej jest nieskończone i nieokresowe. |
| Zbiór liczb rzeczywistych - R | Każdej liczbie rzeczywistej odpowiada na osi liczbowej tylko jeden punkt. Każdemu punktowi na osi liczbowej odpowiada tylko jedna liczba rzeczywista. R = W ∪ IW R = R+ ∪ R− ∪ {0} |
| Związki między zbiorami liczbowymi | 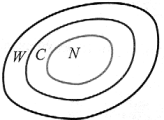  W ∪ IW = R W ∩ IW = Ø N ⊂ C ⊂ W ⊂ R IW ⊂ R |
Działania na zbiorach.
Suma zbiorów
| Sumą zbiorów A i B nazywamy zbiór elementów należących do zbioru A lub do zbioru B. Sumę zbiorów oznaczamy symbolem A ∪ B | 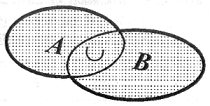 |
Różnica zbiorów
| Różnicą zbiorów A i B nazywamy zbiór złożony z elementów należących do zbioru A i nie należących do zbioru B. Różnicę zbiorów zapisujemy w postaci A \ B | 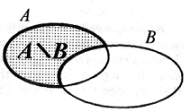 |
Iloczyn zbiorów
| Iloczynem (częścią wspólną) zbiorów A i B nazywamy zbiór elementów należących jednocześnie do zbioru A i do zbioru B. Iloczyn zbiorów zapisujemy symbolem A ∩ B | 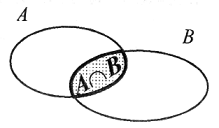 |
Dopełnienie zbioru do przestrzeni
| Jeżeli Ω jest ustalonym zbiorem i A jest podzbiorem właściwym zbioru Ω to różnicę zbiorów Ω i A nazywamy dopełnieniem zbioru A względem zbioru Ω. Dopełnienie zbioru A oznacza się symbolem A'. | 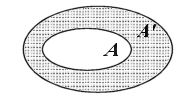 A ∪ A' = Ω A' = Ω \ A |