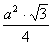Trójkąty jako figury geometryczne płaskie i ich najważniejsze elementy.
Trójkątem nazywamy domkniętą i ograniczoną część płaszczyzny ograniczoną łamaną zwyczajną zamkniętą o trzech bokach - wielokąt o trzech bokach. Jeden z boków, dowolnie wyróżniony, nazywa się podstawą trójkąta, dwa pozostałe ramionami trójkąta. Trójkąt o równych ramionach nazywa się trójkątem równoramiennym. Jeżeli wszystkie boki trójkąta są równe, trójkąt nazywa się trójkątem równobocznym. Boki trójkąta spełniają tzw. warunek trójkąta, tzn. długość dowolnego z nich jest mniejsza od sumy długości boków pozostałych. Liczba równa sumie długości boków trójkąta nazywa się obwodem trójkąta. Kąt wypukły o ramionach zawierających dwa boki trójkąta (również jego miara) nazywa się kątem wewnętrznym trójkąta lub kątem trójkąta. W trójkącie równoramiennym kąty wewnętrzne przy podstawie trójkąta są równe. Jeżeli wszystkie kąty wewnętrzne danego trójkąta są ostre, to trójkąt nazywa się trójkątem ostrokątnym, jeżeli jeden z jego kątów wewnętrznych jest rozwarty - trójkątem rozwartokątnym; jeżeli jeden z kątów wewnętrznych trójkąta jest prosty - trójkątem prostokątnym. Kątem zewnętrznym trójkąta jest kąt przyległy do kąta wewnętrznego trójkąta. Suma miar kątów trójkąta jest równa mierze kąta półpełnego π (180°). Boki i kąty wewnętrzne trójkąta nazywa się elementami trójkąta. Punkt wspólny dwóch boków trójkąta nazywa się wierzchołkiem trójkąta. Trójkąt jest najmniejszą figurą geometryczną wypukłą zawierającą swoje wierzchołki, jest więc dwuwymiarowym sympleksem. Wierzchołek trójkąta i nie zawierający go bok trójkąta nazywa się przeciwległymi. Trójkąt o wierzchołkach A, B, C oznacza się symbolem ΔABC. Odcinek łączący środek boku trójkąta z wierzchołkiem mu przeciwległym nazywa się środkową trójkąta. Środkowe trójkąta przecinają się w jednym punkcie, który dzieli każdą z nich w stosunku 1:2. Punkt przecięcia środkowych trójkąta jest środkiem ciężkości trójkąta.
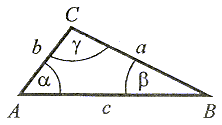 |
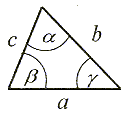
Suma miar kątów wewnętrznych trójkąta jest równa 180°. α + β + δ = 180°. |
Każdy bok trójkąta jest mniejszy od sumy dwóch pozostałych boków tego trójkąta.
|AB| < |AC| + |BC|, |AC| < |AB| + |BC| i |BC| < |AB| + |AC|
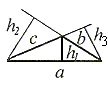
Wysokości trójkąta
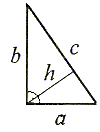
Wysokością trójkąta nazywamu odcinek poprowadzony z wierzchołka trójkąta prostopadle do przeciwległego boku lub do przedłużenia tego boku.
Każdy trójkąt ma trzy wysokości, które przecinają sie w jednym punkcie zwanym ortocentrum (p.O).
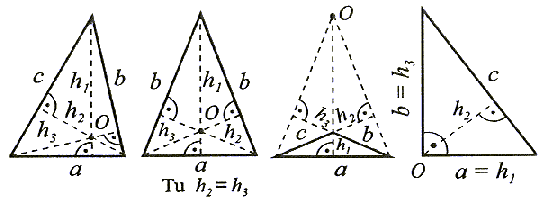
Środkowe boków trójkąta
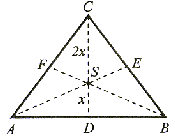 |DS| =  |CD|, |ES| = |CD|, |ES| =  |AE| |AE|oraz |FS| =  |BF| |BF| |
Środkową boku trójkąta nazywamy odcinkiem łączącym środek tego boku z przeciwległym bokiem tego trójkąta. Każdy trójkąt ma trzy srodkowe przecinające się w jednym punkcie (p.S), który nazywamy środkiem ciężkości tego trójkąta. |
Punkt S (środek ciężkości) dzieli każdą środkową w stosunku 1:2, czyli:
|DS| =  |CS|, |ES| =
|CS|, |ES| =  |AS| oraz |FS| =
|AS| oraz |FS| =  |BS|.
|BS|.
Odcinki łączące środki boków trójkąta
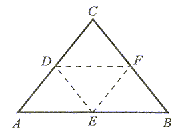 |
Odcinki łączące środki boków trójkąta są równoległe do przeciwległych boków i równe ich połowie. |
DF||AB i |DF| =  |AB|, EF||AC i |EF| =
|AB|, EF||AC i |EF| =  |AC| oraz DE||BC i |DE| =
|AC| oraz DE||BC i |DE| =  |BC|
|BC|
Dwusieczne kątów trójkąta
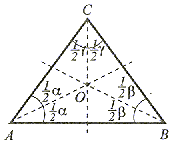 |
Dwusieczna kąta jest to półprosta dzieląca kąt na połowy. Każdy trójkąt ma trzy dwusieczne przecinające się w jednym punkcie (p.O), który jest środkiem koła wpisanego w trójkąt. |
Symetralne boków trójkąta
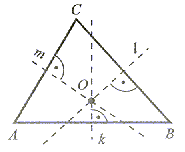 |
Symetralną boku trójkąta nazywamy prostą prostopadłą do tego boku, przechodzącą przez jego środek. Każdy trójkąt ma trzy symetralne boków, przecinające się w jednym punkcie (p.O), który jest środkiem koła opisanego na tym trójkącie |
Środek O koła opisanego na trójkącie może leżeć wewnątrz lub na zewnątrz trójkąta, a w przypadku trójkąta prostokątngo na jego goku (w połowie przeciwprostokątnej).
Trójkąty nie mają środka symetrii.
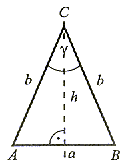 |
Trójkąt równoramienny ma jedną oś symetrii i jest ona jednocześnie dwusieczną kąta (δ) zawartego między ramionami oraz pokrywa się z wysokością figury, symetralną i środkową podstawy. |
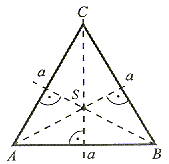 |
Trójkąt równoboczny ma trzy osie symetrii, które są jednocześnie dwusiecznymi kątów, wysokościami, symetralnymi i środkowymi boków figury. |
Punkt przecięcia (C) osi symetrii jest środkiem koła wpisanego i opisanego na trójkącie równobocznym.
Rodzaje trójkątów.
(dowolny) 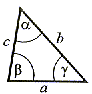 Każdy bok ma inną długość i każdy kąt ma inną miarę. |
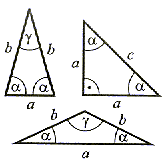 Ma dwa boki równe i nazywamy je ramionami. Trzeci bok to podstawa. Kąty przy podstawie mają tę samą miarę. |
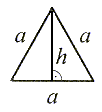
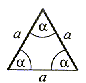 Ma wszystkie boki równej długości. Wszystkie kąty wewnętrzne są równe i mają po 60°. |
(dowolny) 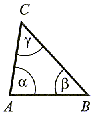 β < 90° δ < 90° Każdy kąt wewnętrzny jest kątem ostrym. |
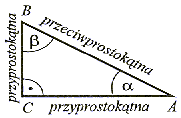 Ma jeden kąt prosty, a dwa pozostałe są ostre i takie, że α + β = 90° |
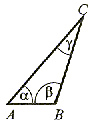 β > 90° δ < 90° Ma jeden kąt rozwarty, a dwa pozostałe są ostre. |
Podział trójkątów ze względu na boki i kąty.
|
ostrokątny |
prostokątny |
rozwartokątny |
|
|
równoboczny (dowolny) |
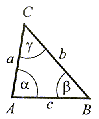 α < 90° β < 90° δ < 90° |
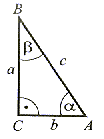 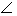 C = 90° C = 90°α + β = 90° |
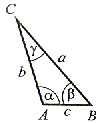 90° < α < 180° α < 90° i β < 90° |
|
równoramienny |
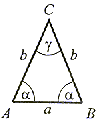 α = β, α < 90° β < 90°, δ < 90° |
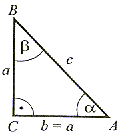 α = β = 45°  C = 90° C = 90° |
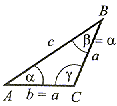 α = β, α < 90° β < 90° 90° < δ < 180° |
|
równoboczny |
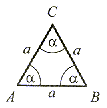 α = 60° |
takiego trójkąta |
takiego trójkąta |
Cechy przystawania trójkątów.
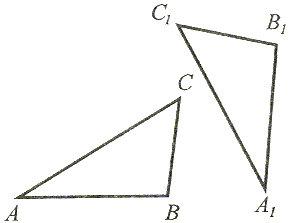 |
Jeżeli boki jednego trójkąta są przystające (równe) do odpowiednich boków drugiego trójkąta, to te trójkąty są przystające. |
|AB| = |A1B1|, |BC| = |B1C1| oraz |AC| = |A1C1|, to  ABC
ABC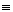
 A1B1C1
A1B1C1
 |
Jeżeli dwa boki i kąt między nimi zawarty jednego trójkąta są przystające (równe) do odpowiednich boków i kąta zawartego między nimi w drugim trójkącie, to te trójkąty są przystające. |
|AB| = |A1B1|, |AC| = |A1C1| i α = α1, to  ABC
ABC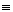
 A1B1C1
A1B1C1
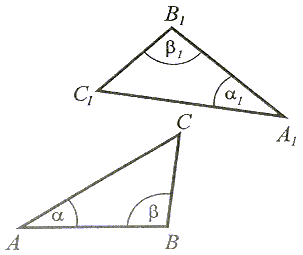 |
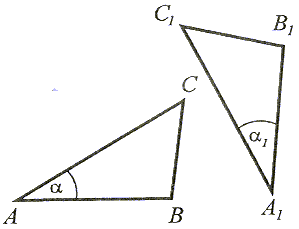
Jeżeli bok i dwa kąty do niego przyległe jednego trójkąta są przystające (równe) do odpowiedniego boku i kątów do niego przyległych w drugim trójkącie, to te trójkąty są przystające. |
|AB| = |A1B1|, α = α1 oraz β = β1, to  ABC
ABC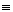
 A1B1C1
A1B1C1
Cechy przystawania trójkątów prostokątnych.
I cecha - Przyprostokątne jednego trójkąta są odpowiednio równe (przystające) przyprostokątnym drugiego trójkąta.
II cecha - Przyprostokątna i kąt ostry do niej przeciwległy jednego trójkąta są odpowiednio równe przyprostokątnej i kątowi do niej przyległemu w drugim trójkącie.
III cecha - Przyprostokątna i kąt do niej przeciwległy jednego trójkąta są odpowiednio równe przyprostokątnej i kątowi do niej przyległemu w drugim trójkącie.
IV cecha -Przeciwprostokątna i jeden z kątów ostrych jednego trójkąta są odpowiednio równe przeciwprostokątnej i jednemu z kątów ostrych w drugim trójkącie.
V cecha -Przeciwprostokątna i jedna z przyprostokątnych jednego trójkąta są odpowiednio równe przeciwprostokątnej i jednej z przyprostokątnych w drugim trójkącie.
Cechy podobieństwa trójkątów.
Własność, która pozwala na określenie podobieństwa pewnej rodziny figur, nazywa się cechą podobieństwa figur tej rodziny.
Wyróżniamy trzy cechy podobieństwa trójkątów:
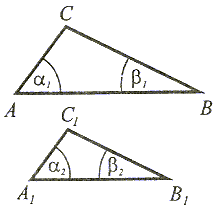 α1 = α2 oraz β1 = β2 |
Jeżeli dwa kąty jednego trójkąta są przystające do odpowiednich kątów drugiego trójkąta, to trójkąty te są podobne. |
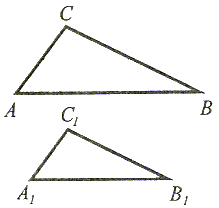 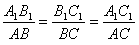 |
Jeżeli stosunki wszystkich boków jednego trójkąta do odpowiednich boków drugiego trójkąta są równe, to trójkąty są podobne. |
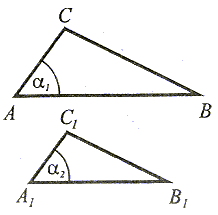 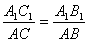 oraz α1 = α |
Jeżeli stosunki dwóch boków jednego trójkąta do odpowiednich boków drugiego trójkąta są równe oraz kąty zawarte między tymi bokami są przystające (równe), to trójkąty te są podobne. |
Cechy podobieństwa trójkątów prostokątnych.
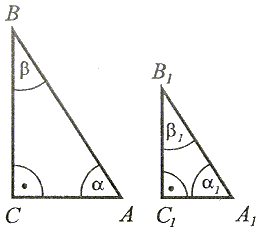 α1 = α lub β1 = β |
Jeżeli dwa trójkąty prostokątne mają po jednym kącie ostrym przystającym, to te trójkąty są przystające. |
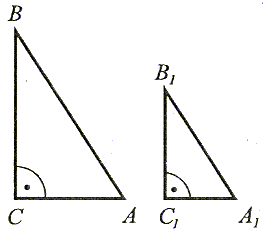 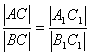 |
Jeżeli stosunek długości przyprostokątnych jednego trójkąta jest równy stosunkowi długości przyprostokątnych drugiego trójkąta, to te trójkąty są podobne. |
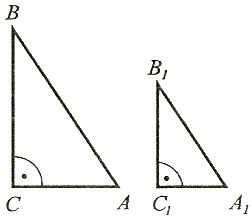 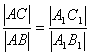 |
Jeżeli stosunek długości przyprostokątnej do długości przeciwprostokątnej jednego trójkąta jest równy stosunkowi odpowiedniej przyprostokątnej do przeciwprostokątnej drugiego trójkąta, to te trójkąty są podobne. |
Można też rozpatrywać stosunki przeciwprostokątnych do odpowiednich przyprostokątnych.
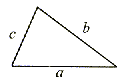
Obwód trójkąta.
|
różnoboczny |
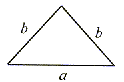
równoranienny |
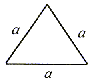
równoboczny |
 |
 |
 |
Pole trójkąta.
|
|
|
|
|
|
|
P = |
P = |
P = |
P = |
P = |
Twierdzenie Pitagorasa.
 |
Jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. |
Twierdzenie odwrotne do twierdzenia Pitagorasa.
Jeżeli w trójkącie o bokach długości a, b i c zachodzi równość a2 + b2 = c2, to trójkąt jest prostokątny.
Okrąg opisany na trójkącie.
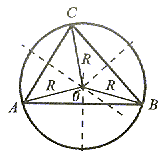 |
Na każdym trójkącie można opisać okrąg. Środkiem okręgu opisanego jest punkt przecięcia się symetralnych boków trójkąta. |
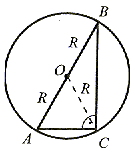 |
Środek okręgu opisanego na trójkącie prostokątnym leży w połowie przeciwprostokątnej. |
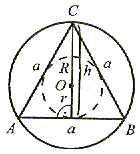 |
Środek okręgu opisanego na trójkącie równobocznym i środek okręgu wpisanegow trójkąt równoboczny pokrywają się. |
Promień okręgu opisanego jest: R = 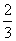 h.
h.
Promień okręgu wpisanego jest: r =  h.
h.
Zależność między obydwoma promieniami: R = 2r.
Geometria.
Geometria jest działem matematyki, który zajmuje się kwestiami kształtu, wielkości, proporcji i relacji kształtów i właściwości w przestrzeni. Geometria jest uważana za jedną z najstarszych nauk matematyki. Proste geometryczne kształty znane były już w paleolicie i zgłębiły je szczegółowo wszystkie starożytne cywilizacje. Geometrię używano pierwotnie dla celów praktycznych, w geodezji i budownictwie. Na poziomie naukowym geometrię stosowali starożytni Grecy.
Ostrosłupy.
Ostrosłupem nazywamy wielościan, którego powierzchnia (brzeg) składa się z wielokąta, nazywanego podstawą ostrosłupa i pewnej liczby trójkątów - ścian bocznych ostrosłupa o wspólnym wierzchołku P nazywanym wierzchołkiem ostrosłupa.
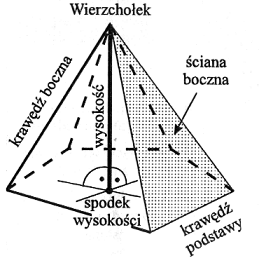 |
Wysokością ostrosłupa nazywamy odcinek prostopadły poprowadzony z wierzchołka ostrosłupa do płaszczyzny podstawy. Ze względu na kształty podstawy wyróżniamy ostrosłupy: trójkątne, czworokątne, pięciokątne itd. |
| Ostrosłup nazywamy foremnym (prawidłowym),jeżeli jego podstawą jest wielokąt foremny, a spodek wysokości leży w środku koła opisanego na podstawie. |
Czworościan foremny
| Czworościanem foremnym nazywamy ostrosłup prawidłowy trójkątny, którego wszystkie ściany są trójkątami równobocznymi. |
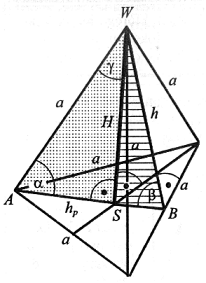 hp = |AB| = 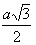 h = 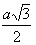 |
H - wysokość ostrosłupa, h - wysokość ściany bocznej, |AB| = hp - wysokość podstawy, gdzie |AS| = 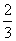 |AB| oraz |BS| = |AB| oraz |BS| =  |AB|, |AB|,α - kąt nachylenia krawędzi bocznej do podstawy, β - kąt nachylenia ściany bocznej do podstawy, δ - kąt między krawędzią boczną i wysokością ostrosłupa, S - spodek wysokości ostrosłupa. |
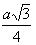 |
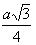 |
Pc = 4 · 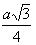 Pc = 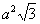 |
 Pp · H, V = Pp · H, V =  · · 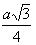 · H · H |
||
Ostrosłup prawidłowy trójkątny
| Ostrosłupem prawidłowym trójkątnym nazywamy ostrosłup, którego podstawą jest trójkąt równoboczny, a ściany boczne są przystającymi trójkątami równoramiennymi. |
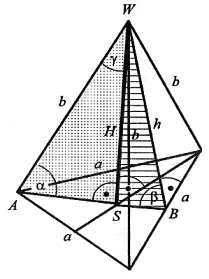 hp = |AB| = 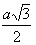 |
H - wysokość ostrosłupa (WS), h - wysokość ściany bocznej(WB), |AB| = hp - wysokość podstawy, gdzie |AS| = 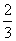 |AB| oraz |BS| = |AB| oraz |BS| =  |AB|, |AB|,α - kąt nachylenia krawędzi bocznej do podstawy, β - kąt nachylenia ściany bocznej do podstawy, δ - kąt między krawędzią boczną i wysokością ostrosłupa, S - spodek wysokości ostrosłupa. |
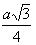 |
 · a · h · a · hPb = 1,5 · a · h |
Pc = 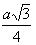 + 1,5 · a · h + 1,5 · a · h |
 Pp · H, V = Pp · H, V =  · · 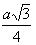 · H · H |
||
Ostrosłup prawidłowy czworokątny
| Ostrosłupem prawidłowym czworokątnym nazywamy ostrosłup, którego podstawą jest kwadrat, a ściany boczne są przystającymi trójkątami równoramiennymi. |
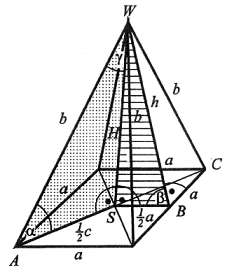 c = 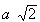 |
H - wysokość ostrosłupa (WS), h - wysokość ściany bocznej(WB), c = |AC| - przekątna podstawy, gdzie |AS| =  c = c = 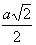 |BS| =  a aα - kąt nachylenia krawędzi bocznej do podstawy, β - kąt nachylenia ściany bocznej do podstawy, δ - kąt między krawędzią boczną i wysokością ostrosłupa, S - spodek wysokości ostrosłupa. |
Pp =  c2 c2 |
 · a · h · a · hPb = 2ah |
Pc = a2 + 2ah |
 Pp · H, V = Pp · H, V =  a2H a2H |
||
Punkt.
Punkt, to jedno z podstawowych pojęć geometrii, element zbioru rozważanego łącznie ze strukturą, wraz z którą zbiór ten tworzy przestrzeń. Punktami nazywa się elementy przestrzeni afinicznej, euklidesowej, metrycznej, itp. W niektórych ujęciach geometrii punkt jest pojęciem pierwotnym.
Punkt okresowy funkcji f to punkt z należący do dziedziny funkcji taki, że dla pewnego n należącego do zbioru liczb naturalnych zachodzi związek fn(x)=x, gdzie fn=f*f*f*...*f (n razy). Najmniejszą liczbę naturalną o tej własności nazywa się okresem punktu x. Punkt okresowy jest punktem stałym n-tej iteracji funkcji f. Punkt okresowyfunkcji jest punktem okresowym generowanego przez nią dyskretnego układu dynamicznego. W 1964r. matematyk ukraiński A.N.Szarkowski udowodnił twierdzenie, z którego wynikało m.in., że jeśłi funkcja ciągła f:<a;b> -> <a;b> ma punkt okresowy o okresie 3, to dla dowolnego n należącego do zbioru liczn naturalnych ma ona punkt okresowy o okresie n.
Punkt osobliwy, punkt nieregularny to element zbioru, nie mający pewnej (ważnej) własności, którą zazwyczaj ma większość punktów badanego zbioru. Najczęściej określenia punktu osobliwego używa się przy rozważaniu własności związanych z różniczkowalnością. Punkt osobliwy krzywej jest to punkt, w którym nie jest określona styczna do krzywej (taki, jak "punkt rozgałęzienia", "ostrze", itp). Podobnie określa się punkt osobliwy na powierzchni.
Graniastosłupy.
Graniastosłup to wielościan, którego wszystkie wierzchołki leżą na dwóch różnych płaszczyznach równoległych, a krawędzie nie zawarte w tych płaszczyznach są równoległe. Płaszczyzny równoległe zawierające wierzchołki graniastosłupa nazywają się płaszczyznami podstaw graniastosłupa. Część wspólna graniastosłupa z każdą z tych płaszczyzn jest jego ścianą - ściany te nazywają się podstawami graniastosłupa. Obie podstawy graniastosłupa przystają do siebie. Boki podstaw graniastosłupa nazywają się krawędziami podstaw graniastosłupa, a pozostałe krawędzie - krawędziami bocznymi graniastosłupa. Każdy odcinek (również jego długość) o końcach leżących na płaszczyznach podstaw graniastosłupa i prostopadły do tych płaszczyzn nazywa się wysokością graniastosłupa. Jeśli krawędzie boczne graniastosłupa są prostopadłe do płaszczyzny podstaw, to taki graniastosłup nazywa się graniastosłupem prostym. Jeśli krawędzie boczne nie są prostopadłe, to graniastosłup nazywa się graniastosłupem pochyłym. Graniastosłup, którego podstawa jest n-kątem, nazywa się graniastosłupem n-kątnym. Graniastosłup prosty, którego podstawą jest wielokąt foremny, nazywa się graniastosłupem prawidłowym. Objętość graniastosłupa jest równa s*h, gdzie s jest polem podstawy graniastosłupa, h - jego wysokością. Przekrojem poprzecznym graniastosłupa nazywa się część wspólną graniastosłupa z płaszczyzną przecinającą wszystkie jego krawędzie boczne. Przekrojem przekątnym graniastosłupa nazywa się część wspólną tego graniastosłupa z płaszczyzną przechodzącą przez jego dwie krawędzie nie należące do jednej ściany. Jeśli płaszczyzna nierównoległa do płaszczyzny podstawy graniastosłupa ma niepustą część wspólną z graniastosłupem, ale nie przecina jego podstaw, to dzieli ona graniastosłup na dwa wielościany, z których każdy nazywa się graniastosłupem ściętym. Podstawami graniastosłupa ściętego są: podstawa przecinanego graniastosłupa i część wspólna graniastosłupa z płaszczyzną przecinającą. Graniastosłup nazywa się graniastosłupem wpisanym w walec, jeśli jego podstawy są wielokątami wpisanymi w podstawy walca. Graniastosłup nazywa się graniastosłupem opisanym na walcu, jeśli jego podstawy są wielokątami opisanymi na podstawach walca.
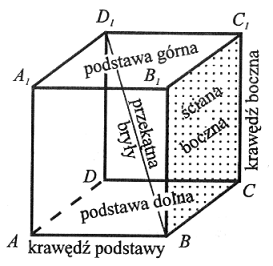 |
Wysokość graniastosłupa jest to odcinek prostopadły do podstaw i zawarty między obydwoma podstawami. Przekątna graniastosłupa jest to odcinek łączący dwa wierzchołki nie leżące na jednej ścianie (np.: BD1). |
Wśród graniastosłupów wyróżniamy:
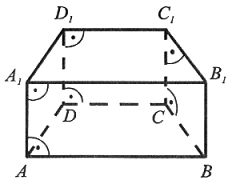 |
Krawędzie boczne graniastosłupów prostych są prostopadłe do obydwóch podstaw, np.: AA1 ⊥ AB i AA1 ⊥ A1B1; CC1 ⊥ DC i CC1 ⊥ D1C1 |
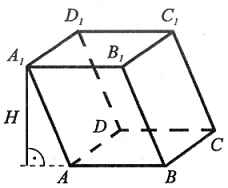 |
Podstawy graniastosłupów pochyłych są równoległe, a krawędzie boczne nie są prostopadłe do podstaw. |
Ze względu na kształt podstawy wyróżniamy graniastosłupy: trójkątne, czworokątne, pięciokątne itd.
| Graniastosłupem prawidłowym nazywamy taki graniastosłup, którego podstawą jest wielokąt foremny (trójkąt równoboczny, kwadrat, pięciokąt foremny, sześciokąt foremny,...). |
Prostopadłościan
| Prostopadłościanem nazywamy graniastosłup prosty, którego wszystkie ściany są prostokątami. |
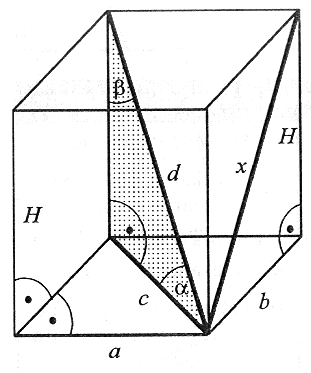 |
a, b - krawędź podstawy, H - wysokość prostopadłościanu (krawędź boczna), c - przekątna podstawy, x - przekątna ściany bocznej, d - przekątna prostopadłościanu, α - kąt nachylenia przekątnej prostopadłościanu do podstawy, β - kąt między krawędzią boczną (wysokością) i przekątną prostopadłościanu. |
Pc = 2ab + 2aH + 2bH |
||
V = a · b · H |
||
Sześcian
| Sześcianem nazywamy prostopadłościan, który ma wszystkie krawędzie równej długości. Jego wszystkie ściany są kwadratami. |
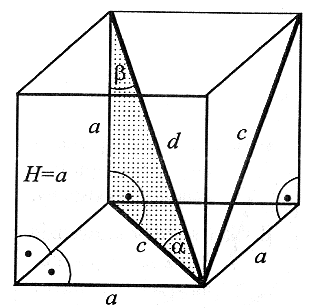 |
a - krawędź sześcianu, c - przekątna podstawy i ściany bocznej (w sześcianie są równe), d - przekątna sześcianu, α - kąt nachylenia przekątnej sześcianu do podstawy, β - kąt między krawędzią boczną i przekątną sześcianu. |
Sześcian jest szczególnym przypadkiem prostopadłościanu.
Pc = 6a2 |
||
V = a3 |
||
Graniastosłup prawidłowy trójkątny
| Graniastosłupem prawidłowym trójkątnym nazywamy graniastosłup, którego podstawą jest trójkąt równoboczny, a jego ściany boczne są przystającymi (równymi) prostokątami. | 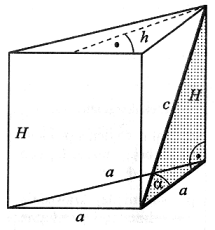 |
a - krawędź podstawy, H - wysokość graniastosłupa, h - wysokość podstawy, c - przekątna ściany bocznej, α - kąt nachylenia przekątnej ściany bocznej do krawędzi podstawy. |
|
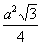 |
Pc = 2 · 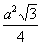 + 3a · H + 3a · H |
|
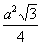 · H · H |
||
Graniastosłup prawidłowy czworokątny
| Graniastosłupem prawidłowym czworokątnym nazywamy graniastosłup, którego podstawą jest kwadrat, a jego ściany boczne są przystającymi (równymi) prostokątami. | 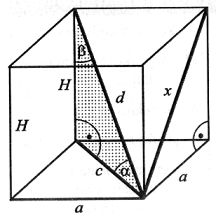 |
a - krawędź podstawy, H - wysokość graniastosłupa, c - przekątna podstawy, d - przekątna graniastosłupa, x - przekątna ściany bocznej α - kąt nachylenia przekątnej graniastosłupa do podstawy, β - kąt pomiędzy krawędzią boczną i przekątną graniastosłupa. |
|
Pc = 2a2 + 4a · H |
||