Analiza matematyczna.
Analiza matematyczna to jeden z podstawowych działów matematyki, w którym główną rolę odgrywają badania rozmaitych funkcji metodami przejść granicznych. Klasyczna analiza obejmuje w szczególności teorię granic ciągów i funkcji, badania ciągłości funkcji, rachunek różniczkowy i całkowy. W XX wieku analiza ogromnie się rozwinęła, do analizy matematycznej (w szerszym sensie) zalicza się różne działy matematyki wyrosłe na jej gruncie, w szczególności analizę funkcjonalną, analizę zespoloną, współczesną geometrię analityczną, teorię równań różniczkowych i całkowych, teorię miary i całki, teorię funkcji rzeczywistych, teorię dystrybucji, rachunek wariacyjny, globalną analizę harmoniczną, analizę na rozmaitościach, teorię układów dynamicznych, a nawet geometrię różniczkową i topologię różniczkową. Nazwa "analiza matematyczna" pochodzi od dawniej używanego terminu "analiza nieskończenie małych", gdyż pierwotnie granice rozważano właśnie używając pojęcia "nieskończenie małe". Rola analizy matematycznej w matematyce jest nietypowa - badania są oparte na wynikach z innych działów:topologii, algebry, teorii mnogości. Z jednej strony analiza bada wiele problemów stawianych głównie w fizyce i mechanice, z drugiej strony zaś ogólne rezultaty analizy znajdują później praktyczne zastosowania. Na potrzeby analizy matematycznej badane są też różnorodne problemy innych działów matematyki, a niektóre dziedziny nawet powstały jako efekt badań analizy (np. teoria mnogości).
Pochodna funkcji to jedno z najważniejszych pojęć analizy matematycznej, mające liczne zastosowania w innych działach matematyki, w naukach przyrodniczych i technicznych.
| |
|
|
 |
||
 |
||
 |
||
 |
 |
 |
 |
||
 |
||
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
|
 |
||
 |
 |
|
 |
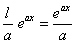 |
|
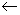 |
 |
|
 |
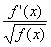 |
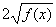 |
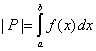 |
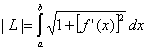 |
|
 |
 |
|
 |
(a+b)3=a3+2a2+3ab2+b3 (a-b)3=a3-3a2b+3ab2-b3 a3+b3=(a+b)(a2)-ab+b2) a3-b3=(a-b)(a2+ab+b2) |
|
 |
||
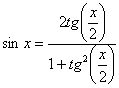 |
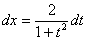 |
|