Ostrosłupy.
Ostrosłupem nazywamy wielościan, którego powierzchnia (brzeg) składa się z wielokąta, nazywanego podstawą ostrosłupa i pewnej liczby trójkątów - ścian bocznych ostrosłupa o wspólnym wierzchołku P nazywanym wierzchołkiem ostrosłupa.
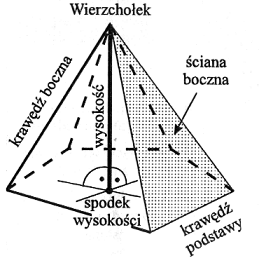 |
Wysokością ostrosłupa nazywamy odcinek prostopadły poprowadzony z wierzchołka ostrosłupa do płaszczyzny podstawy. Ze względu na kształty podstawy wyróżniamy ostrosłupy: trójkątne, czworokątne, pięciokątne itd. |
| Ostrosłup nazywamy foremnym (prawidłowym),jeżeli jego podstawą jest wielokąt foremny, a spodek wysokości leży w środku koła opisanego na podstawie. |
Czworościan foremny
| Czworościanem foremnym nazywamy ostrosłup prawidłowy trójkątny, którego wszystkie ściany są trójkątami równobocznymi. |
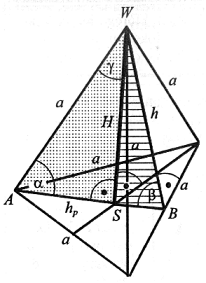 hp = |AB| = 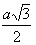 h = 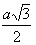 |
H - wysokość ostrosłupa, h - wysokość ściany bocznej, |AB| = hp - wysokość podstawy, gdzie |AS| = 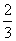 |AB| oraz |BS| = |AB| oraz |BS| =  |AB|, |AB|,α - kąt nachylenia krawędzi bocznej do podstawy, β - kąt nachylenia ściany bocznej do podstawy, δ - kąt między krawędzią boczną i wysokością ostrosłupa, S - spodek wysokości ostrosłupa. |
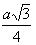 |
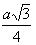 |
Pc = 4 · 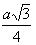 Pc = 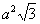 |
 Pp · H, V = Pp · H, V =  · · 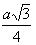 · H · H |
||
Ostrosłup prawidłowy trójkątny
| Ostrosłupem prawidłowym trójkątnym nazywamy ostrosłup, którego podstawą jest trójkąt równoboczny, a ściany boczne są przystającymi trójkątami równoramiennymi. |
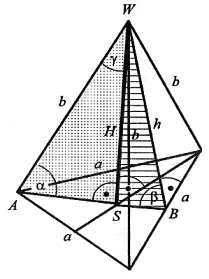 hp = |AB| = 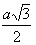 |
H - wysokość ostrosłupa (WS), h - wysokość ściany bocznej(WB), |AB| = hp - wysokość podstawy, gdzie |AS| = 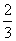 |AB| oraz |BS| = |AB| oraz |BS| =  |AB|, |AB|,α - kąt nachylenia krawędzi bocznej do podstawy, β - kąt nachylenia ściany bocznej do podstawy, δ - kąt między krawędzią boczną i wysokością ostrosłupa, S - spodek wysokości ostrosłupa. |
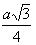 |
 · a · h · a · hPb = 1,5 · a · h |
Pc = 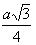 + 1,5 · a · h + 1,5 · a · h |
 Pp · H, V = Pp · H, V =  · · 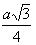 · H · H |
||
Ostrosłup prawidłowy czworokątny
| Ostrosłupem prawidłowym czworokątnym nazywamy ostrosłup, którego podstawą jest kwadrat, a ściany boczne są przystającymi trójkątami równoramiennymi. |
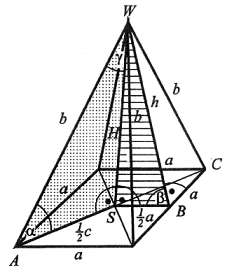 c = 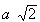 |
H - wysokość ostrosłupa (WS), h - wysokość ściany bocznej(WB), c = |AC| - przekątna podstawy, gdzie |AS| =  c = c = 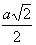 |BS| =  a aα - kąt nachylenia krawędzi bocznej do podstawy, β - kąt nachylenia ściany bocznej do podstawy, δ - kąt między krawędzią boczną i wysokością ostrosłupa, S - spodek wysokości ostrosłupa. |
Pp =  c2 c2 |
 · a · h · a · hPb = 2ah |
Pc = a2 + 2ah |
 Pp · H, V = Pp · H, V =  a2H a2H |
||
Komentarze
Kanał RSS z komentarzami do tego postu.