Rachunek prawdopodobieństwa
Wprowadzenie do rachunku prawdopodobieństwa.
| - |
Rachunek prawdopodobieństwa zaczął się kształtować w XVI wieku gdy zaczęto zauważać pewne prawidłowości w grach hazardowych. Pierwszy dostrzegł je i próbował opisać matematyk włoski Geronimo Cardano (1501-1576). |
| - |
Poważniejszy rozwój rachunku prawdopodobieństwa nastąpił w wieku XVII dzięki pracom P. de Fermat'a i B. Pascal'a (matematycy francuscy). |
| - |
Za twórcę rachunku prawdopodobieństwa jako działu matematyki uważamy szwajcarskiego matematyka Jakuba Bernoullie'go, który opracował te zagadnienia w wieku XVII. |
| - |
Duży wkład i szybki rozwój tej nauki nastąpił w XIX wieku dzięki pracom Gaussa, Laplace'a, Pisson'a, Czybyszewa. |
| - |
Pełnego opracowania i sformalizowania doczekał się rachunek prawdopodobieństwa dopiero w wieku XX dzięki pracom A. Kołogomorowa, matematyka rosyjskiego. |
| - |
Rachunek prawdopodobieństwa stał się podstawą nowoczesnej fizyki - fizyki kwantowej opisującej zachowanie się mikrocząstek. Fizycy kwantowi wykazali, że w świecie mikrocząstek obowiązują prawa probabilistyczne czyli oparte na rachunku prawdopodobieństwa. |
I. Podstawowe pojęcia rachunku prawdopodobieństwa.
| 1. |
Rozważając pewne zdarzenia losowe będziemy określać zbiór zdarzeń elementarnych oznaczanych literką Ω. Są to wszystkie możliwe zdarzenia, które mogą zajść w pewnym doświadczeniu losowym np.: rzut trzykrotnie monetą: Ω={(O,O,O);(O,O,R);(O,R,O);(R,O,O);(R,R,R);(R,R,O);(R,O,R);(O,O,R)} losujemy dwie karty z talii 24 kartowej: Ω={(9  ,9 ,9 )...(9 )...(9 ,A ,A )...(A )...(A ,A ,A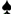 )} )}W matematyce najczęściej każdy obiekt numerujemy co pozwala na wyłączne posługiwanie się liczbami, np. w ostatnim przypadku możemy postąpić następująco: Karty= Wszystkich możliwych par jest bardzo dużo. Zbiór zdarzeń elementarnych można jednak opisać posługując się "domyślnymi" wielokropkami: Ω={(1,2)(1,3)(1,4)....(1,24)(2,1)(2,3)(2,4)....(2,24)....(24,1)(24,2)....(24,23)} |
|||||||||
| 2. |
Bardzo ważna będzie umiejętność przeliczenia ilości zdarzeń elementarnych. Można zdarzenia wypisać i przeliczyć, wypisać z wielokropkami i domyślnie przeliczyć, zastosować pewne zasady lub wzory do przeliczenia ilości zdarzeń. n(Ω) - ilość zdarzeń elementarnych.Dla powyższych przykładów mamy:
|
|||||||||
| 3. |
Wśród zdarzeń elementarnych interesowały nas będą niektóre zdarzenia. Będziemy je nazywali zdarzeniami sprzyjającymi, np. losując 6 liczb w totolotku interesowała nas będzie jakaś wygrana a więc zdarzenie polegające na tym aby wśród sześciu wylosowanych liczb były przynajmniej trzy nasze.
Będziemy musieli przeliczać ilość zdarzeń sprzyjających. W zadaniach wymienionych wyżej będą to następujące ilości:
|
|||||||||
| 4. |
Klasyczna definicja prawdopodobieństwa mówi nam, że prawdopodobieństwo to liczba obliczona ze wzoru: P(A)=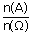 P(A) - prawdopodobieństwo zajścia zdarzenia A n(A) - ilość zdarzeń sprzyjających n(Ω) - ilość zdarzeń elementarnych
|
II. Elementarne zadania.
| Zad.1. | Rzucamy 2-krotnie kostką. Jakie jest prawdopodobieństwo, że suma oczek będzie ≥ 10?
n(Ω)=36 A={(4,6);(5,5);(5,6);(6,6);(6,5);(6,4)} n(A)=6 P(A)= 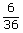 = =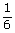 |
||
| Zad.2. |
Ze zbioru cyfr Z losujemy 3 cyfry bez zwracania. Jakie jest prawdopodobieństwo ułożenia z nich (układamy je w kolejności losowania) liczby podzielnej przez 3? z={1,2,3,4}
n(Ω)=24 A={(123)(132)(213)(231)(234)(243)(312)(321)(324)(342)(423)(432)} n(A)=12 P(A)= 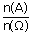 = =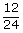 = =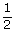 |
III. Matematyczne sposoby opisywania zbiorów i zdarzeń.
Sposoby przeliczania ilości zdarzeń losowych.
| 1. |
Matematyczny sposób opisu zbioru zdarzeń, który będziemy omijać z powodów wymienionych wcześniej.
|
||||||||||||||||||
| 2. |
My będziemy opisywać zbiór słownie a jeśli się da i jest taka potrzeba przez wypisanie jego elementów. W obliczniu prawdopodobieństw matematyczny opis zdarzeń jak już wspominaliśmy do niczego się nie przydaje. Ważna jest - zgodnie ze wzorem na prawdopodobieństwo - ilość zdarzeń w zbiorze. |
||||||||||||||||||
| 3. |
Przeliczanie zbiorów zdarzeń. ω=(a1,a2,a3,...,an) b) podzbiory będziemy oznaczali nawiasem klamrowym ω={z1,z2,z3,...,zn} W podzbiorach elementy nie będą się powtarzać, a kolejność ich wymieniania jest bez znaczenia. |
||||||||||||||||||
| 4. |
Sposoby przeliczania ilości zdarzeń losowych:
ω=(c1,c2,c3...cn) n(Ω)=i1·i2·i3·...·in ik-ilość możliwych zmian na każdym miejscu ciągu. Zilustrujemy to przykładem z zadania nr 2: z={1,2,3,4} n(Ω)=4·3·2=24 n(Ω)=2·2·2·2·2=32 |
||||||||||||||||||
| 5. |
Możliwość stosowania reguły mnożenia do zdarzeń będących podzbiorami. 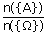 P(A)= 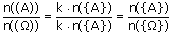 Gdzie: n((Ω))-ilość ciągów n({Ω})-ilość podzbiorów |
| Zadanie 3. | W urnie znajdują się 3 kule białe {1,2,3} oraz 2 czarne {4,5}. Losujemy z urny 2 kule. Oblicz prawdopodobieństwo, że będą jednokolorowe. | ||
| Rozwiązanie I | Rozwiązanie z zastosowaniem podzbiorów. Z={1,2,3,4,5}
n(Ω)=10 n(A)=4 P(A)= 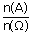 = =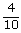 = =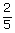 |
||
| Rozwiązanie II |
Rozwiązanie zadania za pomocą ciągów i reguły mnożenia: n(Ω)=5·4=20A={(1,2);(2,1);(1,3);(3,1);(2,3);(3,2);(4,5);(5,4)} n(A)=8 P(A)= 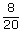 = =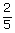 |
IV. Przykładowe zadanie maturalne z rachunku prawdopodobieństwa.
Powyższa elementarna wiedza z rachunku prawdopodobieństwa, pozwala już na rozwiązanie nawet części zadań z poziomu maturalnego.
MATURA II - 2002
| Zadanie 4. | Ze zbioru liczb całkowitych spełniających nierówność x2-8x≤0 |
||
| a) | obliczyć prawdopodobieństwo wylosowania dwóch liczb, których suma wynosi 8, | ||
| b) | obliczyć prawdopodobieństwo wylosowania dwóch liczb pierwszych, | ||
| c) | obliczyć prawdopodobieństwo wylosowania dwóch liczb, których iloczyn jest większy od 10 pod warunkiem, że obie wylosowane liczby są nieparzyste. |
||
| Rozwiązania. | x2-8x≤0 Z={x: x∈R; x2-8x≤0; x∈C} x2-8x≤0 x2-8x=0 Δ=b2-4ac Δ=64 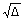 =8 =8x1= 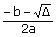 =0 =0x2= 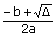 =8 =8x∈<0,8> 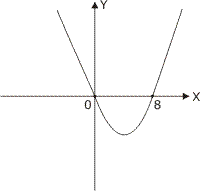 |
||
| a) | Wypisujemy zbiór zdarzeń elementarnych. Zdarzenia sprzyjające podkreślimy. Z={0,1,2,3,4,5,6,7,8}
n(Ω)=8·9=72 n(A)=8 l1+l2=8 P(A)= 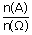 = =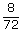 = =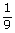 |
||
| b) | Z={2,3,5,7} -liczby pierwsze Wypisujemy zbiór zdarzeń sprzyjających:
n(A)=12 n(Ω)=72 P(A)= 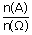 = =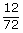 = =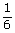 |
||
| c) | Podpunktu c) aktualnie nie będziemy rozwiązywać, gdyż nie znamy pojęcia prawdopodobieństwa warunkowego. |
V. Wzory na przeliczanie zbioru zdarzeń. Zastosowanie.
| 1. | Niektóre zadania jest trudno rozwiązać stosując regułę mnożenia. Niech za przykład posłuży nam zadanie z MATURY 2000 wariant 1 zadanie 5. |
||||||||||||||||||||||||
| Zadanie 5. | W urnach U1 i U2 znajdują się kule oznaczone numerami 1,2,3,4. Skład kul ilustrują diagramy:
|
||||||||||||||||||||||||
| a) | Z urny U1 wylosowano ze zwracaniem 5x po jednej kuli. Jakie jest prawdopodobieństwo, że kulę z numerem 3 wylosowano dwa razy? |
||||||||||||||||||||||||
| b) | Z urny U2 wylosowano kolejno bez zwracania 4 kule. Jakie jest prawdopodobieństwo, że wszystkie wylosowane kule mają inne numery? |
||||||||||||||||||||||||
| c) | Z obu urn wylosowano po jednej kuli. Jakie jest prawdopodobieństwo, że suma numerów wylosowanych kul jest większa niż 3? |
||||||||||||||||||||||||
| Ad. a) | U1 → 5k (ze zwracaniem) n(Ω)=20·20·20·20·20=3 200 000 Jest 5 kul z numerem 3 oraz 15 kul o innych numerach. Ponieważ musimy uwzględnić wystąpienie dwuch kul z nr 3 na dowolnym miejscu ciągu losowania postępujemy następująco: 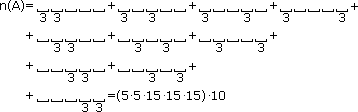 gdyż w każdym składniku sumy występuje ten sam iloczyn choć w różnej kolejności składników. P(A)= 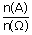 P(A)= 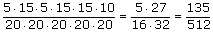 ≈0,26 ≈0,26 |
||||||||||||||||||||||||
| Ad. b) | n(Ω)=24·23·22·21 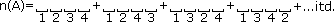 Ze względu na dużą ilość możliwych ustawień "3" reguła mnożenia jest tutaj uciążliwa w zastosowaniu, w związku z czym zrezygnujemy z powyższego sposobu. Można rozwiązać zadanie za pomocą podzbiorów, w których kolejność występowania "3" jest bez znaczenia. Omówimy wzór na przeliczanie takich podzbiorów. Podzbiory k-elementowe losowane ze zbioru n-elementowego (kolejność nieważna) nazywamy kombinacjami. 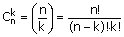 ; ;n! -czytamy "n-silnia" a obliczamy następująco: n!=1·2·3·4·...·n n(Ω)= 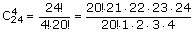 =21·22·23 =21·22·23n(A)= 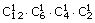 =12·6·4·2 bo =12·6·4·2 bo 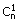 =n =nP(A)= 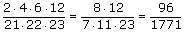 ≈0,05 ≈0,05 |
 =
=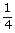
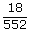 =
=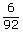 =
=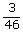
Komentarze
Maturą II 2002
Zadanie 4a
Iiczba zdarzeń możliwych to 64 a nie 72
x2-8x=0
Δ=b2-4ac
Δ=64
a nie 60?
Kanał RSS z komentarzami do tego postu.