Funkcja kwadratowa.
Funkcja kwadratowa (zwana trójmianem kwadratowym), jest to funkcja określona wzorem:
gdzie współczynniki a, b i c są ustalonymi liczbami, przy czym (gdy jest równe zero to mamy funkcję liniową).
Jest to postać ogólna funkcji kwadratowej. Jest to najczęstsza postać występująca w zadaniach matematycznych. Wykresem funkcji kwadratowej jest parabola. Natomiast dziedziną są wszystkie liczby rzeczywiste.
Postać kanoniczna funkcji kwadratowej.
Funkcję kwadratową zawsze można sprowadzić do postaci kanonicznej, wyrażonej wzorem:
.
W postaci kanonicznej jawnie podane mamy współrzędne wierzchołka paraboli W(p, q).
Wyróżnik funkcji kwadratowej.
Liczbę oznaczamy znakiem
i nazywamy wyróżnikiem funkcji kwadratowej.
Postać iloczynowa funkcji kwadratowej.
Jeżeli , to funkcję kwadratową można zapisać w postaci iloczynowej, wyrażonej wzorem:
.
Miejsca zerowe (pierwiastki).
Od wartości wyróżnika funkcji kwadratowej zależy ilość miejsc zerowych posiadanych funkcję kwadratową. I tak jeśli:
istnieją dwa miejsca zerowe:
istnieje jedno podwójne miejsce zerowe:
brak jest rzeczywistych miejsc zerowych.
Wzory Viete'a.
Jeśli liczby x1, x2 są dwoma pierwiastkami funkcji kwadratowej , to mają miejsce następujące wzory Viete'a:
.
Ekstremum i monotoniczność funkcji kwadratowej.
Funkcja kwadratowa ma dokładnie jedno ebstremum dla argumentu , które wynosi
.
W przypadku, gdy a>0 funkcja kwadratowa ma minimum absolutne, a wykresem funkcji jest parabola, któej wierzchołkiem jest punkt , ramiona natomiast są skierowane do góry - funkcja jest malejąca w przedziale
, rosnąca w przedziale
. Jeżeli natomiast a<0, to funkcja kwadratowa ma maksimum absolutne dla
, a wykres jest parabolą o wierzchołku w punkcjie
i ramionach skierowanych do dołu - funkcja jest rosnąca w przedziale
, malejąca w przedziale
.
Dziedzina i zbiór wartości.
Dziedziną funkcji kwadratowej jest zawsze zbiór liczb rzeczywistych .
Funkcja kwadratowa nie jest ograniczona w zbiorze liczb rzeczywistych, ale w zależności od znaku współczynnika a (znak ten bywa nazywany znakiem funkcji kwadratowej) jest ograniczona z dołu (gdy a>0) albi ograniczona z góry (gry a<0). W przypadku gdy , funkcja kwadratowa przyjmuje wartości stałego znaku zgodnie ze znekiem współczynnika a.
Wykres funkcji kwadratowej - parabola.
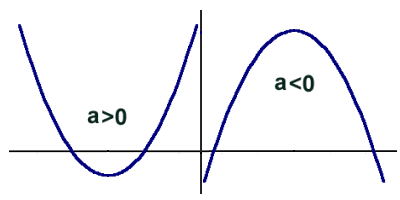
Od współczynnika a zależy w którą stronę skierowane są ramiona paraboli:
- a>0 (dodatnie) - ramiona skierowane w górę, wierzchołek jest minimum funkcji.
- a<0 (ujemne) - ramiona skierowane w dół, wierzchołek jest maksimum funkcji.
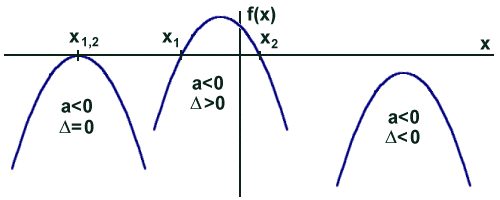
Wykresy funkcji kwadratowej w zależności od parametru a i wyróżnika D: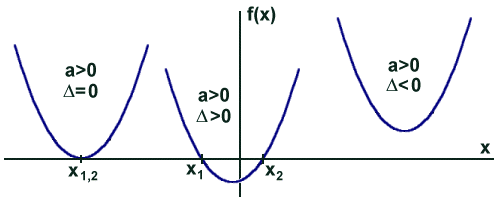
Komentarze
Kanał RSS z komentarzami do tego postu.